Реактивное движение. Уравнение движения тела переменной массы.
Движение некоторых тел сопровождается изменением их массы, например масса ракеты уменьшается за счет истечения газов, образующихся при сгорании топлива, и т. п.
Выведем уравнение движения тела переменной массы на примере движения ракеты. Если в момент времени tмасса ракеты m, а ее скорость v, то по истечении времени dt ее масса уменьшится на dm и станет равной m-dm, а скорость станет равной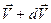 
. Изменение импульса системы за отрезок времени dt
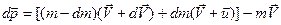
где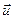 
— скорость истечения газов относительно ракеты. Тогда
( 
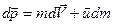
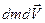— малый высшего порядка малости по сравнению с остальными).
Если на систему действуют внешние силы, то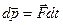 
, поэтому
,
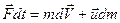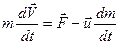, (2-9)
где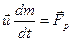
- реактивная сила.
Если 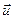противоположен 
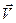, то ракета ускоряется, а если совпадает с 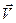, то тормозится.
Таким образом, мы получили уравнение движения тела переменной массы
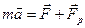. (2-10)
Это уравнение впервые было выведено И. В.Мещерским (1859—1935).
Идея применения реактивной силы для создания летательных аппаратов высказывалась в 1881 г. Н. И. Кибальчичем (1854—1881). К.Э.Циолковский (1857— 1935) в 1903 г. опубликовал статью, где предложил теорию движения ракеты и основы теории жидкостного реактивного двигателя. Поэтому его считают основателем отечественной космонавтики.
Применим уравнение (2-10) к движению ракеты, на которую не действуют никакие внешние силы. Полагая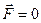 
и считая, что скорость выбрасываемых газов относительно ракеты постоянна (ракета движется прямолинейно), получим
.
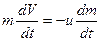
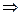
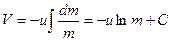Значение постоянной интегрирования С определим из начальных условий. Если в начальный момент времени скорость ракеты равна нулю, а ее стартовая масса то,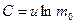 
. Следовательно,
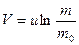. (2-11)
(2-11) называется формулой Циолковского.Из этой формулы следует, что: 1) чем больше конечная масса ракеты m, тем больше должна быть стартовая масса ракеты; 2) чем больше скорость истечения 
газов, тем больше может быть конечная масса при данной стартовой массе ракеты.
Дата добавления: 2015-04-15; просмотров: 905;