Основные определения. Методы штрафных функций относятся к группе непрямых методов решения задач нелинейного программирования:

Методы штрафных функций относятся к группе непрямых методов решения задач нелинейного программирования:

f(x) 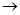min;(7.60)

g_i(x) 0, i 1, ..., k;

h_j(x) 0, j 1, ..., m;

a x b. (7.61)

Они преобразуют задачу с ограничениями в последовательность задач безусловной оптимизации некоторых вспомогательных функций. Последние получаются путем модификации целевой функции с помощью функций-ограничений таким образом, чтобы ограничения в явном виде в задаче оптимизации не фигурировали. Это обеспечивает возможность применения методов безусловной оптимизации. В общем случае вспомогательная функция имеет вид

F(x,a) f(x) +Ф(х, а). (7.62)

Здесь f(x) - целевая функция задачи оптимизации; Ф(х, а) - “штрафная” функция; параметр а 0. Точку безусловного минимума функции F(x, a) будем обозначать через х(а).

В зависимости от вида Ф(х, а) различают методы внутренних штрафных, или барьерных, функций и методы внешних штрафных функций.

Методы внутренних штрафных функций

Эти методы применяются для решения задач нелинейного программирования с ограничениями-неравенствами. В рассматриваемых методах функции Ф(x, а) подбирают такими, чтобы их значения неограниченно возрастали при приближении к границе допустимой области G (рис. 7.12). Иными словами, приближение к границе «штрафуется» резким увеличением значения функции F(x, а). На границе G построен «барьер», препятствующий нарушению ограничении в процессе безусловной минимизации F(x, a). Поиск минимума вспомогательной функции F(x, а) необходимо начинать с внутренней точки области G . При этом в процессе оптимизации траектория спуска никогда не выйдет за пределы допустимой области. Все перечисленные особенности функции Ф (х, а) определили наименование рассматриваемой группы методов.

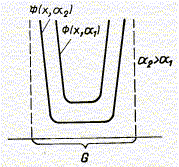
Рис. 7.12 ‑ Внутренняя штрафная функция

Таким образом, внутренняя штрафная функция Ф(х, а) может быть определена следующим образом:

(7.63)

Здесь dG -граница области G.

Общий вид внутренней штрафной функции

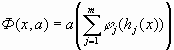, (7.64)

где j _j - непрерывные дифференцируемые функции, определяемые ограничениями-неравенствами исходной задачи нелинейного программирования. Вспомогательная функция F(x, а) при этом имеет форму

. (7.65)

Она определена в области G и неограниченно возрастает, если h_j(х) -> 0 для некоторого j. В качестве внутренних штрафных функций используют, например, такие:

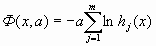; . (7.66)

Алгоритм метода внутренних штрафных функций состоит в следующем. В качестве начальной точки х[0] выбирается произвольная внутренняя точка области G. Задается некоторая монотонно убывающая сходящаяся к нулю последовательность {a_k}, k 1, 2, ..., положительных чисел. Для первого элемента а₁ этой последовательности решается задача безусловной минимизации функции F(x, а), в результате чего определяется точка х(а₁). Эта точка используется в качестве начальной для решения задачи поиска минимума функции F(x, а₂), где а₂ а₁, и т. д. Таким образом, решается последовательность задач безусловной минимизации функций F(х, а_k), k 1, 2, ..., причем решение предыдущей задачи х(а_k) используется в качестве начальной точки для поиска последующего вектора х(а_k+1). Последовательность полученных таким образом точек х(а_k) сходится к оптимальному решению исходной задачи - локальному минимуму х*. Вычисления прекращают при выполнении условий:

|f(x[k]) - f(x[k‑l])| e;(7.67)

||x[k] - x[k‑l]|| b;(7.68)

Здесь e, b - заданные числа, определяющие точность вычислений.

Можно показать, что рассмотренный метод внутренних штрафных функций обладает следующими свойствами:

1) ;

2) 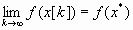и 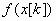монотонно убывает;

3)

Эти свойства справедливы для задач, содержащих непрерывные функции и имеющих локальные минимумы внутри области G.