Основные определения. Задача условной оптимизации заключается в поиске минимального или максимального значения скалярной функции f(x) n-мерного векторного аргументах (в дальнейшем
Задача условной оптимизации заключается в поиске минимального или максимального значения скалярной функции f(x) n-мерного векторного аргументах (в дальнейшем без ограничения общности будут рассматриваться задачи поиска минимального значения функции):
f(x) 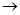 min(7.34)
min(7.34)
при ограничениях:
gi(x)  0, i
0, i  1, ..., k;
1, ..., k;
hj(x)  0, j
0, j  1, .., m;(7.35)
1, .., m;(7.35)
a  x
x  b.
b.
Здесь x, a, b — векторы-столбцы:
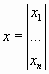 ,
, 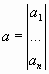 ,
, 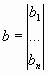 (7.36)
(7.36)
Оптимизируемую функцию f(x) называют целевой функцией. Каждая точка x в n-мерном пространстве переменных x1, ..., х, в которой выполняются ограничения задачи, называется допустимой точкой задачи. Множество всех допустимых точек называется допустимой областью G . Будем считать, что это множество не пусто. Решением задачи считается допустимая точка х*, в которой целевая функция f(х) достигает своего минимального значения. Вектор х* называют оптимальным. Если целевая функция f(x) и ограничения задачи представляют собой линейные функции независимых переменных х1, ..., хn, то соответствующая задача является задачей линейного программировании, в противном случае - задачей нелинейного программирования. В дальнейшем будем полагать, что функции f(x), g(x), i  1, ..., k , hj(x), j
1, ..., k , hj(x), j  1, …, m, - непрерывные и дифференцируемые.
1, …, m, - непрерывные и дифференцируемые.
В общем случае численные методы решения задач нелинейного программирования можно разделить на прямые и непрямые. Прямые методы оперируют непосредственно с исходными задачами оптимизации и генерируют последовательности точек {x[k]}, таких, что f(х[k+1])  f(x[k]). В силу этого такие методы часто называют методами спуска. Математически переход на некотором k-м шаге (k.
f(x[k]). В силу этого такие методы часто называют методами спуска. Математически переход на некотором k-м шаге (k.  0, 1, 2, ...) от точки х[k]к точке x[k+1] можно записать в следующем виде:
0, 1, 2, ...) от точки х[k]к точке x[k+1] можно записать в следующем виде:
x[k+l] x[k] + akp[k], (7.37)
x[k] + akp[k], (7.37)
где р[k] — вектор, определяющий направление спуска; аk — длина шага вдоль данного направления. При этом в одних алгоритмах прямых методов точки х[k] выбираются так, чтобы для них выполнялись все ограничения задачи, в других эти ограничения могут нарушаться на некоторых или всех итерациях. Таким образом, в прямых методах при выборе направления спуска ограничения, определяющие допустимую область G, учитываются в явном виде.
Непрямые методы сводят исходную задачу нелинейного программирования к последовательности задач безусловной оптимизации некоторых вспомогательных функций. При этих методах ограничения исходной задачи учитываются в неявном виде.
Рассмотрим некоторые алгоритмы прямых методов.
Метод проекции градиента
Рассмотрим данный метод применительно к задаче оптимизации с ограничениями-неравенствами. В качестве начальной выбирается некоторая точка допустимой области G. Если х[0] - внутренняя точка множества G (рис. 7.11), то рассматриваемый метод является обычным градиентным методом:
x[k+l]  x[k] –akf’(x[k]), k
x[k] –akf’(x[k]), k  0, 1, 2, ...,(7.38)
0, 1, 2, ...,(7.38)
где 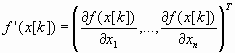 (7.39) ‑ градиент целевой функции f(х) в точке x[k].
(7.39) ‑ градиент целевой функции f(х) в точке x[k].
После выхода на границу области G в некоторой граничной точке х[k] , k  0, 1, 2,..., движение в направлении антиградиента -f’(х[k]) может вывести за пределы допустимого множества (см. рис. 7.11). Поэтому антиградиент проецируется на линейное многообразие М, аппроксимирующее участок границы в окрестности точки х[k]. Двигаясь в направлении проекции вектора -f'(x[k]) на многообразие М, отыскивают новую точку х[k+1], в которой f(х[k+1])
0, 1, 2,..., движение в направлении антиградиента -f’(х[k]) может вывести за пределы допустимого множества (см. рис. 7.11). Поэтому антиградиент проецируется на линейное многообразие М, аппроксимирующее участок границы в окрестности точки х[k]. Двигаясь в направлении проекции вектора -f'(x[k]) на многообразие М, отыскивают новую точку х[k+1], в которой f(х[k+1])  f(x[k]), принимают х[k+1] за исходное приближение и продолжают процесс. Проведем более подробный анализ данной процедуры.
f(x[k]), принимают х[k+1] за исходное приближение и продолжают процесс. Проведем более подробный анализ данной процедуры.

Рис. ‑ 7.11 Геометрическая интерпретация метода проекции градиента
В точке х[k] часть ограничений-неравенств удовлетворяется как равенство:
hi(x)  0, j
0, j  1, ..., l; l
1, ..., l; l  m.
m.
Такие ограничения называют активными.
Обозначим через J набор индексов j(1  j
j  l) этих ограничений. Их уравнения соответствуют гиперповерхностям, образующим границу области G в окрестности точки х[k] . В общем случае эта граница является нелинейной (см. рис. 3.1). Ограничения hj(x), j
l) этих ограничений. Их уравнения соответствуют гиперповерхностям, образующим границу области G в окрестности точки х[k] . В общем случае эта граница является нелинейной (см. рис. 3.1). Ограничения hj(x), j 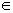 J, аппроксимируются гиперплоскостями, касательными к ним в точке х[k]:
J, аппроксимируются гиперплоскостями, касательными к ним в точке х[k]:
 (7.39)
(7.39)
Полученные гиперплоскости ограничивают некоторый многогранник М, аппроксимирующий допустимую область G в окрестности точки х[k] (см. рис. 7.11).
Проекция р[k] антиградиента ‑f'(x[k]) на многогранник вычисляется по формуле
p[k]  P[‑f’(x[k])].(7.40)
P[‑f’(x[k])].(7.40)
Здесь Р ‑ оператор ортогонального проектирования, определяемый выражением
Р  E – AT(AAT)-1A,(7.41)
E – AT(AAT)-1A,(7.41)
где Е ‑ единичная матрица размеров п; А - матрица размеров lхn . Она образуется транспонированными векторами-градиентами аj, j  1, ..., l, активных ограничений. Далее осуществляется спуск в выбранном направлении:
1, ..., l, активных ограничений. Далее осуществляется спуск в выбранном направлении:
x[k+1]  x[k] + akp[k].(7.42)
x[k] + akp[k].(7.42)
Можно показать, что точка х[k+1] является решением задачи минимизации функции f(х) в области G тогда и только тогда, когда
Р[‑f’(x[k])]  0,(7.43)
0,(7.43)
т. е 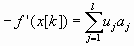 , (7.44)
, (7.44)
и u  (u1, ..., ul)
(u1, ..., ul)  (ATA)-1AT(-f’(х[k]))
(ATA)-1AT(-f’(х[k]))  0.(7.45)
0.(7.45)
Эти условия означают, что антиградиент (-f’(х[k])) целевой функции является линейной комбинацией с неотрицательными коэффициентами градиентов ограничений hj(x)  0.
0.
В соответствии с изложенным алгоритм метода проекции градиента состоит из следующих операций.
1. В точке х[k] определяется направление спуска р[k].
2. Находится величина шага аk.
3. Определяется новое приближение х[k+1].
Рассмотрим детально каждую из этих операций.
1. Определение направления спуска состоит в следующем. Пусть найдена некоторая точка х[k] 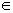 G и известен набор активных ограничений hi(х[k])
G и известен набор активных ограничений hi(х[k])  0, j
0, j 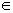 J. На основании данной информации вычисляют (-f’(х[k])) и определяют проекцию Р[-f’(х[k])]. При этом возможны два случая:
J. На основании данной информации вычисляют (-f’(х[k])) и определяют проекцию Р[-f’(х[k])]. При этом возможны два случая:
а) Р[‑f’(х[k])] не равна 0. В качестве направления спуска р[k] принимают полученную проекцию;
б) Р[-f’(х[k])]  0, т. е.
0, т. е. 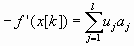 . (7.46)
. (7.46)
Данное выражение представляет собой систему из п уравнений для определения коэффициентов иj. Если все иj  0, j
0, j 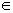 J, то в соответствии с вышеизложенным точка х[k] является решением задачи. Если же некоторый компонент иq
J, то в соответствии с вышеизложенным точка х[k] является решением задачи. Если же некоторый компонент иq  0, то соответствующий ему градиент выводится из матрицы А и порождается новая проецирующая матрица Р. Она определит новое направление спуска.
0, то соответствующий ему градиент выводится из матрицы А и порождается новая проецирующая матрица Р. Она определит новое направление спуска.
2. Для определения величины шага аk целевая функция минимизируется по направлению р[k] при условии соблюдения ограничений задачи с установленной точностью. Последняя задается введением некоторого положительного числа e. Считают, что точка х удовлетворяет условиям задачи с заданной точностью, если hi(х)  e, j
e, j  1, ..., m. Величина шага аk определяется решением задачи вида:
1, ..., m. Величина шага аk определяется решением задачи вида:
f(x[k] + ар[k]) > min;(7.47)
hj(x[k] + ар[k])  e, j
e, j  1, ..., m.(7.48)
1, ..., m.(7.48)
3. Определение нового приближения состоит в следующем. Очередная точка вычисляется по формуле
x[k+1]  x[k] + аkр[k]. (7.49)
x[k] + аkр[k]. (7.49)
Признаком сходимости является стремление к нулю векторов р[k]. Рассмотренный метод является в некотором смысле аналогом градиентных методов для решения задач на безусловный экстремум, и ему свойствен их недостаток - медленная сходимость.
Комплексный метод Бокса
Этот метод представляет модификацию метода деформируемого многогранника и предназначен для решения задачи нелинейного программирования с ограничениями-неравенствами. Для минимизации функции n переменных f(x) в n-мерном пространстве строят многогранники, содержащие q  п+1 вершин. Эти многогранники называют комплексами, что и определило наименование метода.
п+1 вершин. Эти многогранники называют комплексами, что и определило наименование метода.
Введем следующие обозначения:
х[j, k]  (х1[j, k], …, хi[j, k], …, хn[j, k])T, (7.50)
(х1[j, k], …, хi[j, k], …, хn[j, k])T, (7.50)
где j  1, ..., q; k
1, ..., q; k  0, 1, 2, ... - j-я вершина комплекса на k-м этапе поиска;
0, 1, 2, ... - j-я вершина комплекса на k-м этапе поиска;
х[h, k] - вершина, в которой значение целевой функции максимально, т. е. f(x[h, k])  max{f(x[l, k]), ..., f(x[q, k])}; x[h, k]- центр тяжести всех вершин, за исключением х[h, k] . Координаты центра тяжести вычисляются по формуле
max{f(x[l, k]), ..., f(x[q, k])}; x[h, k]- центр тяжести всех вершин, за исключением х[h, k] . Координаты центра тяжести вычисляются по формуле
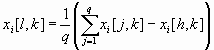 , i
, i  l, ..., n.(7.51)
l, ..., n.(7.51)
Алгоритм комплексного поиска состоит в следующем. В качестве первой вершины начального комплекса выбирается некоторая допустимая точка х[1, 0]. Координаты остальных q-1 вершин комплекса определяются соотношением
хj[j, 0]  аi + ri(bi - ai), i
аi + ri(bi - ai), i  1, ..., п; j
1, ..., п; j  2, ..., q.(7.52)
2, ..., q.(7.52)
Здесь аi, bi - соответственно нижнее и верхнее ограничения на переменную хi', ri - псевдослучайные числа, равномерно распределенные на интервале [0, 1]. Полученные таким образом точки удовлетворяют ограничениям а  х
х  b , однако ограничения hj(x)
b , однако ограничения hj(x)  0 могут быть нарушены. В этом случае недопустимая точка заменяется новой, лежащей в середине отрезка, соединяющего недопустимую точку с центром тяжести выбранных допустимых вершин. Данная операция повторяется до тех пор, пока не будут выполнены все ограничения задачи. Далее, как и в методе деформируемого многогранника, на каждой итерации заменяется вершина х[h, k], в которой значение целевой функции имеет наибольшую величину. Для этого х[h, k] отражается относительно центра тяжести х[l, k] остальных вершин комплекса. Точка х[р, k], заменяющая вершину х[h, k], определяется по формуле
0 могут быть нарушены. В этом случае недопустимая точка заменяется новой, лежащей в середине отрезка, соединяющего недопустимую точку с центром тяжести выбранных допустимых вершин. Данная операция повторяется до тех пор, пока не будут выполнены все ограничения задачи. Далее, как и в методе деформируемого многогранника, на каждой итерации заменяется вершина х[h, k], в которой значение целевой функции имеет наибольшую величину. Для этого х[h, k] отражается относительно центра тяжести х[l, k] остальных вершин комплекса. Точка х[р, k], заменяющая вершину х[h, k], определяется по формуле
x[p, k]  (a+1)х[l, k] + ax[h, k],(7.53)
(a+1)х[l, k] + ax[h, k],(7.53)
где а  0 - некоторая константа, называемая коэффициентом отражения. Наиболее удовлетворительные результаты дает значение а
0 - некоторая константа, называемая коэффициентом отражения. Наиболее удовлетворительные результаты дает значение а  1,3. При этом новые вершины комплекса отыскиваются за небольшое количество шагов, а значения целевой функции уменьшаются достаточно быстро.
1,3. При этом новые вершины комплекса отыскиваются за небольшое количество шагов, а значения целевой функции уменьшаются достаточно быстро.
Если f(x[р, k])  f(x[h, k]), то новая вершина оказывается худшей вершиной комплекса, В этом случае коэффициент а уменьшается в два раза. Если в результате отражения нарушается какое-либо из ограничений, то соответствующая переменная просто возвращается внутрь нарушенного ограничения. Если при отражении нарушаются ограничения hj(x)
f(x[h, k]), то новая вершина оказывается худшей вершиной комплекса, В этом случае коэффициент а уменьшается в два раза. Если в результате отражения нарушается какое-либо из ограничений, то соответствующая переменная просто возвращается внутрь нарушенного ограничения. Если при отражении нарушаются ограничения hj(x)  0. то коэффициент а каждый раз уменьшается вдвое до тех пор, пока точка х[р, k] не станет допустимой. Вычисления заканчиваются, если значения целевой функции мало меняются в течение пяти последовательных итераций: |f(х[l, k+1]) – f(х [l, k])|
0. то коэффициент а каждый раз уменьшается вдвое до тех пор, пока точка х[р, k] не станет допустимой. Вычисления заканчиваются, если значения целевой функции мало меняются в течение пяти последовательных итераций: |f(х[l, k+1]) – f(х [l, k])|  e, k
e, k  1, ..., 5, где e - заданная константа. В этом случае центр тяжести комплекса считают решением задачи нелинейного программирования.
1, ..., 5, где e - заданная константа. В этом случае центр тяжести комплекса считают решением задачи нелинейного программирования.
Достоинствами комплексного метода Бокса являются его простота, удобство для программирования, надежность в работе. Метод на каждом шаге использует информацию только о значениях целевой функции и функций ограничений задачи. Все это обусловливает успешное применение его для решения различных задач нелинейного программирования.
Выбор начальной точки допустимой области
Для применения прямых методов решения задач нелинейного программирования требуется знание некоторой допустимой начальной точки области G . Если структура этой области сложная, отыскание такой точки представляет серьезные трудности. Произвольно выбранная начальная точка в общем случае может удовлетворять только части ограничений. Следовательно, необходим алгоритм, приводящий из произвольной точки в допустимую область. На практике для получения начального вектора применяют тот же метод, которым решают исходную задачу нелинейного программирования. Рассмотрим один из способов отыскания такого вектора.
Пусть 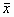 ‑ произвольная точка, в которой часть ограничений не удовлетворяется. Обозначим через J1 множество индексов ограничений, выполняющихся в точке
‑ произвольная точка, в которой часть ограничений не удовлетворяется. Обозначим через J1 множество индексов ограничений, выполняющихся в точке 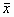 , и через J2 - множество индексов ограничений, не выполняющихся в ней, т.е.
, и через J2 - множество индексов ограничений, не выполняющихся в ней, т.е.
J1  {j|hj(
{j|hj( 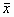 )
)  0, j
0, j  1, …, m};(7.54)
1, …, m};(7.54)
J2  {j|hj(
{j|hj( 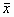 )
)  0, j
0, j  1, …, m};(7.55)
1, …, m};(7.55)
Введем дополнительную переменную z и сформулируем задачу поиска допустимой точки следующим образом: найти минимум функции z  z при ограничениях:
z при ограничениях:
hj(х)  0, j
0, j 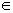 J1;
J1;
hj(х) - z  0, j
0, j 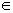 J2;(7.57)
J2;(7.57)
Допустимый вектор этой задачи находится довольно просто. Действительно, если положить
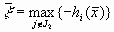 ,(7.58)
,(7.58)
то точка  является допустимым решением сформулированной задачи. Так как область G исходной задачи не пуста, то существует такая точка
является допустимым решением сформулированной задачи. Так как область G исходной задачи не пуста, то существует такая точка 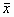 , что
, что
h(x)  0, j
0, j  1, …, m. (7.59)
1, …, m. (7.59)
Следовательно, минимальное значение z меньше нуля. В силу этого после конечного числа шагов некоторого прямого алгоритма будут получены x[0], z, такие, что z  0, и условия задачи удовлетворяются. Точка х[0] и принимается в качестве начальной для исходной задачи нелинейного программирования.
0, и условия задачи удовлетворяются. Точка х[0] и принимается в качестве начальной для исходной задачи нелинейного программирования.
Дата добавления: 2015-04-03; просмотров: 1314;
