Минимизация функций многих переменных. Основные положения
Градиентом дифференцируемой функции f(x) в точке х[0] называется n-мерный вектор f(x[0]), компоненты которого являются частными производными функции f(х), вычисленными в точке х[0], т. е.
f'(x[0]) = (дf(х[0])/дх1, …, дf(х[0])/дхn)T. (7.11)
Этот вектор перпендикулярен к плоскости, проведенной через точку х[0] , и касательной к поверхности уровня функции f(x), проходящей через точку х[0] .В каждой точке такой поверхности функция f(x) принимает одинаковое значение. Приравнивая функцию различным постоянным величинам С0, С1, ... , получим серию поверхностей, характеризующих ее топологию (рис. 7.8).
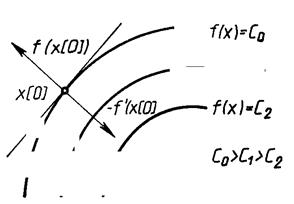
Рис. 7.8 ‑ Градиент
Вектор-градиент направлен в сторону наискорейшего возрастания функции в данной точке. Вектор, противоположный градиенту
( 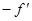 (х[0])), называется антиградиентом и направлен в сторону наискорейшего убывания функции. В точке минимума градиент функции равен нулю. На свойствах градиента основаны методы первого порядка, называемые также градиентным и методами минимизации. Использование этих методов в общем случае позволяет определить точку локального минимума функции.
(х[0])), называется антиградиентом и направлен в сторону наискорейшего убывания функции. В точке минимума градиент функции равен нулю. На свойствах градиента основаны методы первого порядка, называемые также градиентным и методами минимизации. Использование этих методов в общем случае позволяет определить точку локального минимума функции.
Очевидно, что если нет дополнительной информации, то из начальной точки х[0] разумно перейти в точку х [1], лежащую в направлении антиградиента - наискорейшего убывания функции. Выбирая в качестве направления спуска р[k] антиградиент 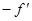 (х[k]) в точке х[k], получаем итерационный процесс вида
(х[k]) в точке х[k], получаем итерационный процесс вида
х[k+1] = x[k]‑akf'(x[k]), аk > 0; k=0, 1, 2, ...
В координатной форме этот процесс записывается следующим образом:
xi[k+1]=хi[k] ‑ ak 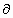 f(x[k])/
f(x[k])/ 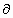 xi
xi
i = 1, ..., n; k= 0, 1, 2,...
В качестве критерия останова итерационного процесса используют либо выполнение условия малости приращения аргумента || x[k+l] - x[k] || <= e, либо выполнение условия малости градиента
|| 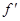 (x[k+l]) || <= g,
(x[k+l]) || <= g,
Здесь e и g - заданные малые величины.
Возможен и комбинированный критерий, состоящий в одновременном выполнении указанных условий. Градиентные методы отличаются друг от друга способами выбора величины шага аk.
При методе с постоянным шагом для всех итераций выбирается некоторая постоянная величина шага. Достаточно малый шаг аk обеспечит убывание функции, т. е. выполнение неравенства
f(х[k+1]) = f(x[k] – akf’(x[k])) < f(x[k]).
Однако это может привести к необходимости проводить неприемлемо большое количество итераций для достижения точки минимума. С другой стороны, слишком большой шаг может вызвать неожиданный рост функции либо привести к колебаниям около точки минимума (зацикливанию). Из-за сложности получения необходимой информации для выбора величины шага методы с постоянным шагом применяются на практике редко.
Более экономичны в смысле количества итераций и надежности градиентные методы с переменным шагом, когда в зависимости от результатов вычислений величина шага некоторым образом меняется. Рассмотрим применяемые на практике варианты таких методов.
Метод наискорейшего спуска
При использовании метода наискорейшего спуска на каждой итерации величина шага аk выбирается из условия минимума функции f(x) в направлении спуска, т. е. f(x[k] –akf’(x[k])) = 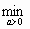 f(x[k] – af'(x[k])).
f(x[k] – af'(x[k])).
Это условие означает, что движение вдоль антиградиента происходит до тех пор, пока значение функции f(x) убывает. С математической точки зрения на каждой итерации необходимо решать задачу одномерной минимизации по а функции j(a) = f(x[k] - af'(x[k])) .
Алгоритм метода наискорейшего спуска состоит в следующем.
1. Задаются координаты начальной точки х[0].
2. В точке х[k], k = 0, 1, 2, ... вычисляется значение градиента f’(x[k]).
3. Определяется величина шага ak, путем одномерной минимизации по а функции j(a) = f(x[k] - af'(x[k])).
4. Определяются координаты точки х[k+1]:
хi[k+1] = xi[k] – аkf’i(х[k]), i = 1 ,..., п.
5. Проверяются условия останова стерационного процесса. Если они выполняются, то вычисления прекращаются. В противном случае осуществляется переход к п. 1.
В рассматриваемом методе направление движения из точки х[k] касается линии уровня в точке x[k+1] (рис. 7.9). Траектория спуска зигзагообразная, причем соседние звенья зигзага ортогональны друг другу. Действительно, шаг ak выбирается путем минимизации по а функции ?(a) = f(x[k] - af'(x[k])). Необходимое условие минимума функции dj(a)/da = 0. Вычислив производную сложной функции, получим условие ортогональности векторов направлений спуска в соседних точках:
dj(a)/da = -f’(x[k+1] 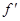 (x[k]) = 0.
(x[k]) = 0.
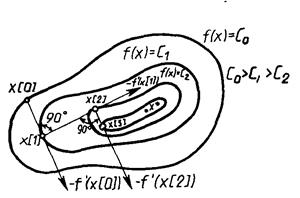
Рис. 7.9 ‑ Геометрическая интерпретация метода наискорейшего спуска
Градиентные методы сходятся к минимуму с высокой скоростью (со скоростью геометрической прогрессии) для гладких выпуклых функций. У таких функций наибольшее М и наименьшее m собственные значения матрицы вторых производных (матрицы Гессе)
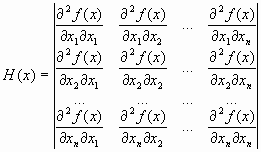 (7.12)
(7.12)
мало отличаются друг от друга, т. е. матрица Н(х) хорошо обусловлена. Напомним, что собственными значениями li, i =1, …, n, матрицы являются корни характеристического уравнения
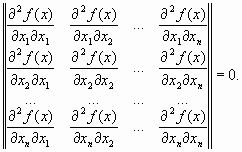 (7.13)
(7.13)
Однако на практике, как правило, минимизируемые функции имеют плохо обусловленные матрицы вторых производных (т/М << 1). Значения таких функций вдоль некоторых направлений изменяются гораздо быстрее (иногда на несколько порядков), чем в других направлениях. Их поверхности уровня в простейшем случае сильно вытягиваются (рис. 7.10), а в более сложных случаях изгибаются и представляют собой овраги. Функции, обладающие такими свойствами, называют овражными. Направление антиградиента этих функций (см. рис. 7.10) существенно отклоняется от направления в точку минимума, что приводит к замедлению скорости сходимости.
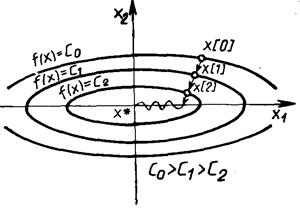
Рис. 7.10 ‑ Овражная функция
Скорость сходимости градиентных методов существенно зависит также от точности вычислений градиента. Потеря точности, а это обычно происходит в окрестности точек минимума или в овражной ситуации, может вообще нарушить сходимость процесса градиентного спуска. Вследствие перечисленных причин градиентные методы зачастую используются в комбинации с другими, более эффективными методами на начальной стадии решения задачи. В этом случае точка х[0] находится далеко от точки минимума, и шаги в направлении антиградиента позволяют достичь существенного убывания функции.
Метод сопряженных градиентов
Рассмотренные выше градиентные методы отыскивают точку минимума функции в общем случае лишь за бесконечное число итераций. Метод сопряженных градиентов формирует направления поиска, в большей мере соответствующие геометрии минимизируемой функции. Это существенно увеличивает скорость их сходимости и позволяет, например, минимизировать квадратичную функцию
f(x) = (х, Нх) + (b, х) + а
с симметрической положительно определенной матрицей Н за конечное число шагов п , равное числу переменных функции. Любая гладкая функция в окрестности точки минимума хорошо аппроксимируется квадратичной, поэтому методы сопряженных градиентов успешно применяют для минимизации и неквадратичных функций. В таком случае они перестают быть конечными и становятся итеративными.
По определению, два n-мерных вектора х и у называют сопряженными по отношению к матрице H (или H-сопряженными), если скалярное произведение (x, Ну) = 0. Здесь Н ‑ симметрическая положительно определенная матрица размером п на п.
Одной из наиболее существенных проблем в методах сопряженных градиентов является проблема эффективного построения направлений. Метод Флетчера-Ривса решает эту проблему путем преобразования на каждом шаге антиградиента -f(x[k]) в направление p[k], H-сопряженное с ранее найденными направлениями р[0], р[1], ..., р[k‑1]. Рассмотрим сначала этот метод применительно к задаче минимизации квадратичной функции.
Направления р[k] вычисляют по формулам:
p[k] = 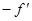 (x[k])+bk-1p[k-l], k >= 1;
(x[k])+bk-1p[k-l], k >= 1;
p[0] = 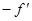 (x[0]).
(x[0]).
Величины bk-1 выбираются так, чтобы направления p[k], р[k‑1] были H-сопряженными:
(p[k], Hp[k-1])= 0.
В результате для квадратичной функции
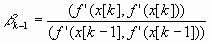 ,
,
итерационный процесс минимизации имеет вид
x[k+l] =x[k] +akp[k],
где р[k] - направление спуска на k-м шаге; аk - величина шага. Последняя выбирается из условия минимума функции f(х) по а в направлении движения, т. е. в результате решения задачи одномерной минимизации:
f(х[k] + аkр[k]) = 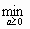 f(x[k] + ар [k]).
f(x[k] + ар [k]).
Для квадратичной функции
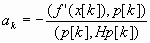 (7.14)
(7.14)
Алгоритм метода сопряженных градиентов Флетчера-Ривса состоит в следующем.
1. В точке х[0] вычисляется p[0] = ‑f’(x[0]).
2. На k-м шаге по приведенным выше формулам определяются шаг аk. и точка х[k+1].
3. Вычисляются величины f(x[k+1]) и f’(x[k+1]).
4. Если 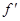 (x[k+1]) = 0, то точка х[k+1] является точкой минимума функции f(х). В противном случае определяется новое направление p[k+l] из соотношения
(x[k+1]) = 0, то точка х[k+1] является точкой минимума функции f(х). В противном случае определяется новое направление p[k+l] из соотношения
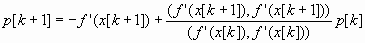 (7.15)
(7.15)
и осуществляется переход к следующей итерации. Эта процедура найдет минимум квадратичной функции не более чем за п шагов. При минимизации неквадратичных функций метод Флетчера-Ривса из конечного становится итеративным. В таком случае после (п+1)-й итерации процедуры 1-4 циклически повторяются с заменой х[0] на х[п+1] , а вычисления заканчиваются при 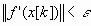 , где
, где 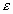 - заданное число. При этом применяют следующую модификацию метода:
- заданное число. При этом применяют следующую модификацию метода:
x[k+l] = x[k] +akp[k],
p[k] = -f’(x[k])+bk-1p[k‑l], k >= 1;
p[0] = ‑ 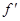 (x[0]);
(x[0]);
f(х[k] + akp[k]) = 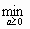 f(x[k] + ap[k];
f(x[k] + ap[k];
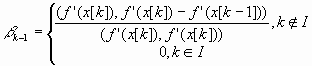 . (7.16)
. (7.16)
Здесь I- множество индексов: I = {0, n, 2п, Зп, ...}, т. е. обновление метода происходит через каждые п шагов.
Геометрический смысл метода сопряженных градиентов состоит в следующем (рис. 7.11). Из заданной начальной точки х[0] осуществляется спуск в направлении р[0] = ‑f'(x[0]). В точке х[1] определяется вектор-градиент f'(x [1]). Поскольку х[1] является точкой минимума функции в направлении р[0], то f’(х[1]) ортогонален вектору р[0]. Затем отыскивается вектор р [1], H-сопряженный к р [0] . Далее отыскивается минимум функции вдоль направления р[1] и т. д.
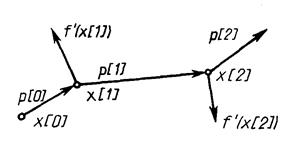
Рис. 7.11 ‑ Траектория спуска в методе сопряженных градиентов
Методы сопряженных направлений являются одними из наиболее эффективных для решения задач минимизации. Однако следует отметить, что они чувствительны к ошибкам, возникающим в процессе счета. При большом числе переменных погрешность может настолько возрасти, что процесс придется повторять даже для квадратичной функции, т. е. процесс для нее не всегда укладывается в п шагов.
Численные методы безусловной оптимизации второго порядка
Дата добавления: 2015-04-03; просмотров: 2699;
