Общая характеристика методов нулевого порядка

В этих методах для определения направления спуска не требуется вычислять производные целевой функции. Направление минимизации в данном случае полностью определяется последовательными вычислениями значений функции. Следует отметить, что при решении задач безусловной минимизации методы первого и второго порядков обладают, как правило, более высокой скоростью сходимости, чем методы нулевого порядка. Однако на практике вычисление первых и вторых производных функции большого количества переменных весьма трудоемко. В ряде случаев они не могут быть получены в виде аналитических функций. Определение производных с помощью различных численных методов осуществляется с ошибками, которые могут ограничить применение таких методов. Кроме того, на практике встречаются задачи, решение которых возможно лишь с помощью методов нулевого порядка, например задачи минимизации функций с разрывными первыми производными. Критерий оптимальности может быть задан не в явном виде, а системой уравнений. В этом случае аналитическое или численное определение производных становится очень сложным, а иногда невозможным. Для решения таких практических задач оптимизации могут быть успешно применены методы нулевого порядка. Рассмотрим некоторые из них.

Метод прямого поиска (метод Хука-Дживса)

Суть этого метода состоит в следующем. Задаются некоторой начальной точкой х[0]. Изменяя компоненты вектора х[0], обследуют окрестность данной точки, в результате чего находят направление, в котором происходит уменьшение минимизируемой функции f(x). В выбранном направлении осуществляют спуск до тех пор, пока значение функции уменьшается. После того как в данном направлении не удается найти точку с меньшим значением функции, уменьшают величину шага спуска. Если последовательные дробления шага не приводят к уменьшению функции, от выбранного направления спуска отказываются и осуществляют новое обследование окрестности и т. д.

Алгоритм метода прямого поиска состоит в следующем.

1. Задаются значениями координат х_i[0] , i = 1, ..., п , начальной точки х[0], вектором изменения координат D х в процессе обследования окрестности, наименьшим допустимым значением е компонентов D х.

2. Полагают, что х[0] является базисной точкой х^б, и вычисляют значение f(x^б).

3. Циклически изменяют каждую координату х^б_i, i = 1, ..., п , базисной точки х^б на величину Dх_i, i = 1, ..., п , т. е. х_i[k] = х^б + D х; х_i[k]= х^б_i - ?х_i. При этом вычисляют значения f(x[k]) и сравнивают их со значением f(x^б). Если f(x[k]) < f(x^б), то соответствующая координата х_i, i = 1, ..., п , приобретает новое значение, вычисленное по одному из приведенных выражений. В противном случае значение этой координаты остается неизменным. Если после изменения последней п-йкоординаты f(x[k]) < f(x^б), то переходят к п, 4. В противном случае ‑ к п. 7.

4. Полагают, что х[k] является новой базисной точкой х^б , и вычисляют значение f(x^б).

5. Осуществляют спуск из точки х[k] > х_i[k+1] = 2х_i[k] ‑ x^б, i = 1, ..., n , где x^б - координаты предыдущей базисной точки. Вычисляют значение f(x[k+1]).

6. Как и в п. 3, циклически изменяют каждую координату точки х[k+1], осуществляя сравнение соответствующих значений функции f(х) со значением f (х[k+1]), полученным в п. 5. После изменения последней координаты сравнивают соответствующее значение функции f(x[k]) со значением f(x^б), полученным в п. 4. Если f(x[k]) < f(x^б), то переходят к п. 4, в противном случае ‑ к п. 3. При этом в качестве базисной используют последнюю из полученных базисных точек.

7. Сравнивают значения D х и е. Если D х < е, то вычисления прекращаются. В противном случае уменьшают значения D х и переходят к п. 3.

Достоинством метода прямого поиска является простота его программирования на компьютере. Он не требует знания целевой функции в явном виде, а также легко учитывает ограничения на отдельные переменные, а также сложные ограничения на область поиска.

Недостаток метода прямого поиска состоит в том, что в случае сильно вытянутых, изогнутых или обладающих острыми углами линий уровня целевой функции он может оказаться неспособным обеспечить продвижение к точке минимума. Действительно, в случаях, изображенных на Рис. 7.4, а и б, каким бы малым ни брать шаг в направлении х₁ или x₂ из точки х’ нельзя получить уменьшения значения целевой функции.

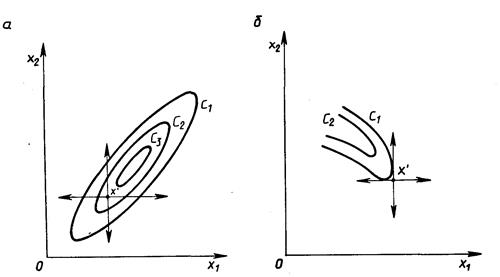
Рис. 7.4 ‑ Прямой поиск: невозможность продвижения к минимуму:

а – С₁ > C₂ > C₃; б ‑ С₁ > C₂

Напомним, что поверхностью уровня (на плоскости ‑ линией уровня) является поверхность, получаемая приравниванием выражения функции f(х) некоторой постоянной величине С, т. е. f(х) = С . Во всех точках этой поверхности функция имеет одно и то же значение С. Давая величине С различные значения С₁, ..., С_n, получают ряд поверхностей, геометрически иллюстрирующих характер функции.

Метод деформируемого многогранника (метод Нелдера—Мида)

Данный метод состоит в том, что для минимизации функции п переменных f(х) в n-мерном пространстве строится многогранник, содержащий (п + 1)вершину. Очевидно, что каждая вершина соответствует некоторому вектору х. Вычисляются значения целевой функции f(х) в каждой из вершин многогранника, определяются максимальное из этих значений и соответствующая ему вершина х[h]. Через эту вершину и центр тяжести остальных вершин проводится проецирующая прямая, на которой находится точка х[q] с меньшим значением целевой функции, чем в вершине х[h] (рис. 7.5). Затем исключается вершина х[h]. Из оставшихся вершин и точки x[q] строится новый многогранник, с которым повторяется описанная процедура. В процессе выполнения данных операций многогранник изменяет свои размеры, что и обусловило название метода.

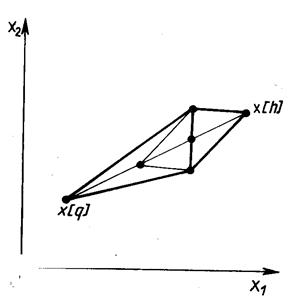
Рис. 7.5 ‑ Геометрическая интерпретация метода деформируемого многогранника

Введем следующие обозначения:

x[i, k] =(x₁[i, k], …, x_j[i, k], …, x_n[i, k])^T

где i = 1, ..., п + 1; k = 0, 1, ..., - i-я вершина многогранника на k-м этапе поиска; х[h, k] — вершина, в которой значение целевой функции максимально, т. е. f(х[h, k] = max{f(x[1, k]), …, f(x[n+1, k])}; х[l, k] - вершина, в которой значение целевой функции минимально, т. е. f(х[l, k]) =min {f(x[1, k]), …, f(x [n+1, k])}; х [п+2, k]- центр тяжести всех вершин, за исключением х[h, k]. Координаты центра тяжести вычисляются по формуле

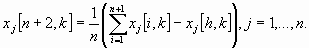
Алгоритм метода деформируемого многогранника состоит в следующем.

1. Осуществляют проецирование точки х[h, k] через центр тяжести:

x[n+3, k] =x[n+2, k] + a(x[n+2, k] - x[h, k]) ,

где а > 0 - некоторая константа. Обычно а = 1.

2. Выполняют операцию растяжения вектора х[n+3, k] - х[n+2, k]:

x[n+4, k] =x[n+2, k] + g(x[n+3, k] - x[n+2, k]),

где g > 1 - коэффициент растяжения. Наиболее удовлетворительные результаты получают при 2,8 <= g <= 3.

Если f(x[n+4, k]) < f(х[l, k]), то х[h , k] заменяют на x[n+4, k] и продолжают вычисления с п. 1 при k = k + 1. В противном случае х[h, k] заменяют на х[n+3, k] и переходят к п. 1 при k = k + 1.

3. Если f(x[n+3, k]) > f(х[i, k]) для всех i, не равных h, то сжимают вектор x[h, k] - x[n+2, k]:

x[n+5, k] =x[n+2, k] + b (х[h, k] – x[n+2, k] ), где b > 0 - коэффициент сжатия. Наиболее хорошие результаты получают при 0,4 <= b <= 0,6.

Затем точку х[h, k] заменяют на х[n+5, k] и переходят к п. 1 при k = k+ 1.

4. Если f(x[n+3, k])> f(x[h, k]), то все векторы х[i, k] - х[l, k] . i= 1,..., п + 1, уменьшают в два раза:

x[i, k] = x[l, k] + 0,5(x[i, k] - x[l, k]) .

Затем переходят к п. 1 при k= k + 1.

В диалоговой системе оптимизации выход из подпрограммы, реализующей метод деформируемого многогранника, осуществляется при предельном сжатии многогранника, т. е. при выполнении условия

, (7.10)

где e = (е₁ ,..., е_n) ‑ заданный вектор.

С помощью операции растяжения и сжатия размеры и форма деформируемого многогранника адаптируются к топографии целевой функции. В результате многогранник вытягивается вдоль длинных наклонных поверхностей, изменяет направление в изогнутых впадинах, сжимается в окрестности минимума, что определяет эффективность рассмотренного метода.

Метод вращающихся координат (метод Розенброка)

Суть метода состоит во вращении системы координат в соответствии с изменением скорости убывания целевой функции. Новые направления координатных осей определяются таким образом, чтобы одна из них соответствовала направлению наиболее быстрого убывания целевой функции, а остальные находятся из условия ортогональности. Идея метода состоит в следующем (рис. 7.6).

Рис. 7.6 ‑ Геометрическая интерпретация метода Розенброка

Из начальной точки х[0] осуществляют спуск в точку х[1] по направлениям, параллельным координатным осям. На следующей итерации одна из осей должна проходить в направлении y₁ = х[1] ‑ х[0], а другая - в направлении, перпендикулярном к у₁ . Спуск вдоль этих осей приводит в точку х[2] , что дает возможность построить новый вектор х[2] ‑ х[1] и на его базе новую систему направлений поиска. В общем случае данный метод эффективен при минимизации овражных функций, так как результирующее направление поиска стремится расположиться вдоль оси оврага.

Алгоритм метода вращающихся координат состоит в следующем.

1. Обозначают через р₁[k], ..., р_n[k] направления координатных осей в некоторой точке х[k] (на к-й итерации). Выполняют пробный шаг h₁ вдоль оси р₁[k], т. е.

x[kl] = x[k] + h₁p₁[k].

Если при этом f(x[kl]) < f(x[k]), то шаг h умножают на величину b > 1;

Если f(x[kl]) > f(x[k]), - то на величину (-b), 0 < |b| < 1;

x[kl] = x[k] + b h₁p₁[k].

Полагая ?h₁ = а₁ .получают

x[kl] = x[k] + a₁p₁[k].

2. Из точки х[k1] выполняют шаг h₂ вдоль оси р₂[k]:

x[k2] = x[k] + a₁p₁[k] + h₂p₂[k].

Повторяют операцию п. 1, т. е.

x[k2] =x[k] + а₁р₁[k] +а₂p₂[k].

Эту процедуру выполняют для всех остальных координатных осей. На последнем шаге получают точку

х[kn] = х[k+1] = х[k] + .

3. Выбирают новые оси координат p₁[k+1], …, р_n[k+1]. В качестве первой оси принимается вектор

р₁[k+1] = x[k+l] ‑ x[k].

Остальные оси строят ортогональными к первой оси с помощью процедуры ортогонализации Грама - Шмидта. Повторяют вычисления с п. 1 до удовлетворения условий сходимости.

Коэффициенты b подбираются эмпирически. Хорошие результаты дают значения b = - 0,5 при неудачных пробах (f(x[ki]) > f(x[k])) и b = 3 при удачных пробах (f(x[ki]) < f(x[k])).

В отличие от других методов нулевого порядка алгоритм Розенброка ориентирован на отыскание оптимальной точки в каждом направлении, а не просто на фиксированный сдвиг по всем направлениям. Величина шага в процессе поиска непрерывно изменяется в зависимости от рельефа поверхности уровня. Сочетание вращения координат с регулированием шага делает метод Розенброка эффективным при решении сложных задач оптимизации.

Метод параллельных касательных (метод Пауэлла)

Этот метод использует свойство квадратичной функции, заключающееся в том, что любая прямая, которая проходит через точку минимума функции х*, пересекает под равными углами касательные к поверхностям равного уровня функции в точках пересечения (рис. 7.7).

Этот метод использует свойство квадратичной функции, заключающееся в том, что любая прямая, которая проходит через точку минимума функции х*, пересекает под равными углами касательные к поверхностям равного уровня функции в точках пересечения (рис. 7.7).

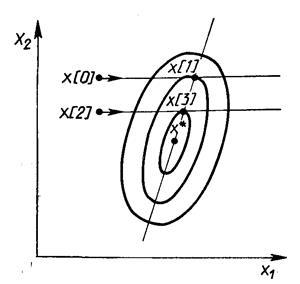
Рис. 7.7 ‑ Геометрическая интерпретация метода Пауэлла

Суть метода такова. Выбирается некоторая начальная точка х[0] и выполняется одномерный поиск вдоль произвольного направления, приводящий в точку х[1] . Затем выбирается точка х[2], не лежащая на прямой х[0] - х[1], и осуществляется одномерный поиск вдоль прямой, параллельной х[0] - х[1],. Полученная в результате точка х[3] вместе с точкой х[1] определяет направление x[1] ‑ х[3] одномерного поиска, дающее точку минимума х^*. В случае квадратичной функции n переменных оптимальное значение находится за п итераций. Поиск минимума при этом в конечном счете осуществляется во взаимно сопряженных направлениях. В случае неквадратичной целевой функции направления поиска оказываются сопряженными относительно матрицы Гессе. Алгоритм метода параллельных касательных состоит в следующем.

1. Задаются начальной точкой x[0]. За начальные направления поиска р[1], ..., р[0] принимают направления осей координат, т. е. р [i] = е[i], i = 1, ..., n (здесь e[i]= (0, ..., 0, 1, 0, … 0)^T).

2. Выполняют n одномерных поисков вдоль ортогональных направлений р[i] , i = 1, ..., п. При этом каждый следующий поиск производится из точки минимума, полученной на предыдущем шаге. Величина шага а_k находится из условия

f(x[k] + а_kр[k]) = 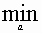f(x[k] + ар[k]).

Полученный шаг определяет точку

х[k+1] = х[k] + а_kр[k] .

3. Выбирают новое направление p =‑x[n] ‑ х[0] и заменяют направления р[1], ..., р[n] на р[2], ..., р [n], р. Последним присваивают обозначения р[1], ..., р[n]

4. Осуществляют одномерный поиск вдоль направления р = р[n] = х[n] - х[0]. Заменяют х[0] на х[n+1] = х[n] + а_nр[п] и принимают эту точку за начальную точку х[0] для следующей итерации. Переходят к п. 1.

Таким образом, в результате выполнения рассмотренной процедуры осуществляется поочередная замена принятых вначале направлений поиска. В итоге после n шагов они окажутся взаимно сопряженными.

Численные методы безусловной оптимизации первого порядка