Плазменный электролиз воды
Вводная часть
Энергетическая эффективность воды не ограничивается получением из неё дешевого водорода. В последние годы проведено большое количество экспериментов, доказывающих возможность получения дополнительной тепловой энергии из воды. Происходит это в процессах кавитации воды и воздействия импульсного тока на её ионы и кластеры.
Ниже мы опишем серию экспериментов, которые показывают, что вода может генерировать значительное количество дополнительной тепловой энергии, выявление которой блокировалось ошибочным электротехническим законом сохранения энергии. Мы продолжим анализ этой ошибочности, чтобы специалистам было легче разобраться в её сути.
Плазменный электролиз воды
Первый в мире патент на плазмоэлектролитическую ячейку был получен в СССР в 1987 г [21]. Самая простая плазмоэлектролитическая ячейка представлена на рис. 78. Её корпус изготовлен из диэлектрического материала. Раствор в ячейку подаётся снизу через трубчатый катод 5. Так как площадь анода 3 значительно больше работающей площади двух катодов 4 и 5, то в зонах (Р-Р) катодов возникает плазма.
Поскольку в плазме идут хаотические процессы, то её сопротивление меняется также хаотически. Осциллограммы напряжения (рис. 79), тока (рис. 80) и мощности (рис. 81), полученные с помощью электронного осциллографа «Handyscope - 2», подтверждают это.
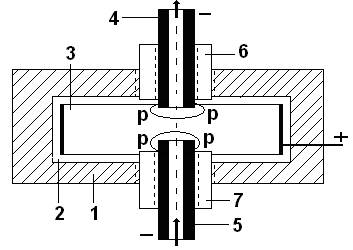
Рис. 78. Схема плазмоэлектролитической ячейки (патент № 2157862):
1-корпус ячейки, 3-анод, 4-катод (выпускной патрубок),
5-катод (впускной патрубок), 6 и 7 – втулки; Р-Р – зоны плазмы
Вполне естественно, что возникают сложности в точном измерении напряжения и тока на клеммах плазмоэлектроитической ячейки, поэтому мы уделим внимание этому вопросу и покажем, что игнорирование противоречий в показаниях различных приборов долгое время скрывало значительные резервы уменьшения затрат электрической энергии при её импульсном потреблении из сети. Первичный источник сетевой энергии – генератор электростанции, питающий тысячи потребителей. Это значительно усложняет проверку ошибочности электротехнического закона сохранения энергии, согласно которому величина энергии или мощности на клеммах потребителя не может быть больше величины электрической энергии, забираемой из сети.
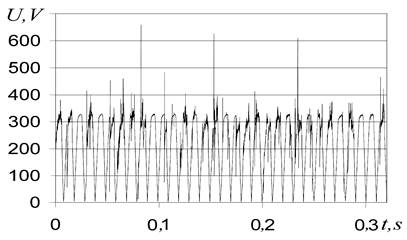
Рис. 79. Осциллограмма напряжения в сети питания плазмоэлектролитической ячейки
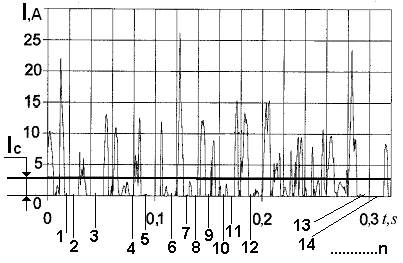
Рис. 80. Осциллограмма тока в цепи питания плазмоэлектролитической ячейки
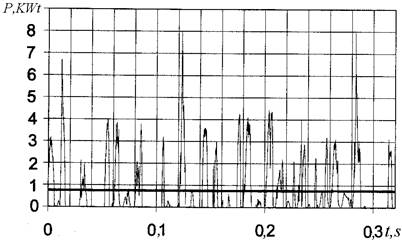
Рис. 81. Осциллограмма мощности в цепи питания плазмоэлектролитической ячейки
Как видно (рис. 79), амплитуды импульсов выпрямленного сетевого напряжения превышают 300В. Такое напряжение названо действующим. Оно также непрерывно, как и сетевое синусоидальное напряжение. Поэтому математическая программа, обрабатывая эту осциллограмму, выдаст среднюю величину напряжения без учета моментов времени, когда величина тока (рис. 80) равняется нулю, а напряжение не участвует в этот момент в формировании средней величины мощности. В результате средняя величина оказывается равной не средней величине напряжения, периодически участвующего в формировании мощности, а средней величине, непрерывно генерируемого напряжения. Особо отметим, что до сих пор нет понимающих ошибочность сложившейся процедуры учета напряжения в формировании импульсной мощности, забираемой из сети (рис. 81) [3], [4].
Считается, что перемножение средних значений напряжения 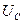 и тока
и тока 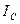 даёт в этом случае достоверную величину средней мощности
даёт в этом случае достоверную величину средней мощности 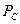 . Поскольку сетевой источник энергии не ограничен в своих возможностях питать одновременно большое количество потребителей, то указанную ошибку почти невозможно зарегистрировать экспериментально. Попытайтесь убедить в этом авторов ошибочных математических программ, закладываемых в электроизмерительные приборы. Они тут же сообщат Вам, что их программы позволяют измерять в секунду десятки тысяч ординат и выдают сверхточную среднюю величину меняющегося напряжения (
. Поскольку сетевой источник энергии не ограничен в своих возможностях питать одновременно большое количество потребителей, то указанную ошибку почти невозможно зарегистрировать экспериментально. Попытайтесь убедить в этом авторов ошибочных математических программ, закладываемых в электроизмерительные приборы. Они тут же сообщат Вам, что их программы позволяют измерять в секунду десятки тысяч ординат и выдают сверхточную среднюю величину меняющегося напряжения ( 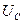 - средняя величина напряжения не показана на рис. 79) и тока (
- средняя величина напряжения не показана на рис. 79) и тока ( 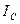 - средняя величина тока показана на рис. 80).
- средняя величина тока показана на рис. 80).
Если спросить у математиков, как их программа, заложенная, например, в осциллограф учитывает интервалы времени неучастия напряжения в формировании мощности, когда ток (рис. 80) равен нулю, то они не поймут необходимость такого учёта. Интервалы времени, когда ток равен нулю, отмечены на осциллограмме тока (рис. 80) цифрами 1,2,3, ………n. В эти интервалы времени напряжение не участвует в формировании мощности, поэтому требуется введение скважности для учёта этого неучастия, но оно отсутствует в математической модели (32). В результате средняя величина мощности оказывается увеличенной в количество раз, равное скважности импульсов напряжения.
Суть отмеченного наиболее ярко представляется при импульсном расходе электрической энергии с большой скважностью импульсов. Многие импульсные эксперименты по нагреванию воды импульсами напряжения и тока мы проводили в течение 5мин. или 300с со скважностью импульсов напряжения и тока, равной 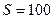 . Из формулы (32) следует, что при импульсном токе среднее напряжение (300 В) остаётся неизменным в процессе всего эксперимента 300с (рис. 82). Это значит, что при однократном делении произведения амплитуд напряжения и тока на скважность (32) одна из перемножаемых величин остаётся на клеммах ячейки постоянной. В этом случае или вольтметр должен показывать 300В, или амперметр – 50А в течение 300 с (рис. 82).
. Из формулы (32) следует, что при импульсном токе среднее напряжение (300 В) остаётся неизменным в процессе всего эксперимента 300с (рис. 82). Это значит, что при однократном делении произведения амплитуд напряжения и тока на скважность (32) одна из перемножаемых величин остаётся на клеммах ячейки постоянной. В этом случае или вольтметр должен показывать 300В, или амперметр – 50А в течение 300 с (рис. 82).
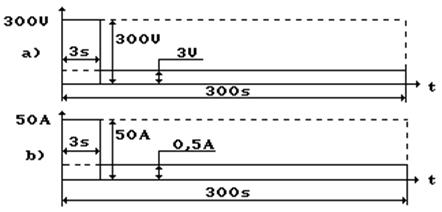
Рис. 82. Схема времени действия максимальных (300В, 50А) и
средних (3,0В, 0,5А) значений напряжения и тока
При скважности импульсов, равной 100 и длительности эксперимента 300с энергия в ячейку подаётся 300/100 всего 3 сек, а 297с ячейка не получает энергию, что и является причиной столь небольшой величины средней импульсной мощности. Все приборы, подключённые к клеммам ячейки, отказываются подчиняться математическим программам определения средней мощности по формуле (32) и указывают её величину, соответствующую формуле (31), но математики игнорируют это фундаментальное противоречие [1], [5].
Мы не будем повторять анализ сути физической ошибки, заложенной в формуле (32). Желающие знать её могут прочесть в главе 14 монографии «Начала физхимии микромира» http://www.micro-world.su/ , а мы продолжим анализ процесса получения дополнительной тепловой энергии из воды. Опишем результаты различных экспериментов по получению из воды дополнительной тепловой энергии ячейками, которые потребляют электроэнергию из сети в виде импульсов напряжения и тока с большой (до 100) скважностью импульсов.
На рис. 83 представлена вольтамперная характеристика плазмоэлектролитической ячейки, работавшей с одномолярным раствором соляной кислоты HCl. Энергии связи валентного электрона атома хлора представлены в табл. 18, а результаты эксперимента – в табл. 17.
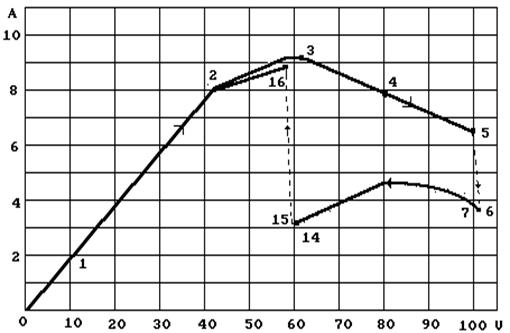
Рис. 83. Вольтамперная характеристика, соответствующая таблице 17
Таблица 17. Результаты эксперимента при расходе 1-нормального раствора HCl 8,74 л/час и его температуре на входе 23,0 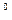 C
C
| Ном. точки | Напря-жение, V | Сила тока, A | Энерг. на входе, kJ | Темп. воды на выходе, С | Энерг. на выходе kJ | Показ. Эффек. % |
| 1,7 | 61,2 | 36,6 | 59,8 | |||
| 8,2 | 1180,8 | 952,1 | 80,6 | |||
| 58,5 | 9,15 | 1927,0 | 1831,0 | 95,0 | ||
| 7,85 | 2260,8 | 2160,6 | 95,6 | |||
| 6,65 | 2394,0 | 83,5 | 2215,5 | 93,0 | ||
| 3,75 | 1377,0 | 2121,1 | 154,0 | |||
| 4,7 | 1438,2 | 1684,5 | 117,1 | |||
| 4,3 | 1176,5 | 1538,0 | 130,7 | |||
| 68,5 | 3,75 | 924,7 | 1171,8 | 126,7 | ||
| 4,5 | 1425,6 | 1757,8 | 123,3 | |||
| 4,2 | 1391,0 | 1757,8 | 126,4 | |||
| 4,4 | 1489,0 | 71,5 | 1776,1 | 119,3 | ||
| 4,2 | 1481,8 | 1757,8 | 118,6 | |||
| 3,9 | 954,7 | 1208,5 | 126,6 | |||
| 3,3 | 760,3 | 988,7 | 130,0 | |||
| 3,05 | 669,8 | 842,3 | 126,0 | |||
| 57,5 | 9,3 | 1925,1 | 1794,4 | 93,2 |
Примечание: энергии выделяющихся газов водорода и кислорода, а также излучаемого света, не учитывались.
При повышении напряжения линейно, в соответствии с законом Ома, растет сила тока (рис. 83 и табл. 17). Затем, при напряжении более 40 Вольт линейность изменения тока нарушается, а при напряжении около 100 Вольт (точки 5 - 6) сила тока уменьшается скачкообразно, и у катода появляется яркое свечение (плазма). Дальнейшее принудительное уменьшение напряжения (точки 6 - 15) незначительно изменяет силу тока. При напряжении около 60 Вольт (точки 14 - 15) свечение у катода исчезает, сила тока скачкообразно увеличивается почти до прежней величины [32].
Таблица 18. Спектр 1-го электрона атома хлора
| Значения | n | |||||
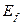 (эксп.) (эксп.)
| eV | 9,08 | 11,25 | 12,02 | 12,34 | 12,53 |
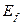 (теор.) (теор.)
| eV | 9,08 | 11,24 | 11,99 | 12,34 | 12,54 |
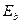 (теор.) (теор.)
| eV | 3,89 | 1,72 | 0,97 | 0,62 | 0,43 |
Энергия на входе в ячейку определялась по показаниям вольтметра и амперметра наивысших классов точности, а на выходе - по разности температур раствора, прошедшего через ячейку.
Вольтамперная характеристика индивидуальна для каждой ячейки и режима её работы. Она зависит от конструктивных параметров ячейки, используемых материалов катода и анода, концентрации и химического состава раствора, а также от его расхода (рис. 84).
Чтобы выяснить влияние расхода раствора на вольтамперную характеристику, были проведены специальные эксперименты при разном расходе раствора KOH (рис. 84).
Во всех трех группах экспериментов устойчивая плазма у катода появляется при напряжении около 100 Вольт и исчезает при понижении напряжения до 85 Вольт. В период существования плазмы наблюдался интенсивный выход парогазовой смеси.
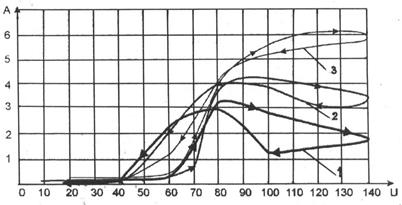
Рис. 84. Вольтамперные характеристики плазмоэлектролитического реактора при расходе раствора КОН: 1 – 3,6 л/ч; 2 – 8,2 л/ч; 3 – 12,2 л/ч
Как видно на рис. 84, вольтамперные характеристики представляют собой двойные петли. Анализ рис. 84 показывает, что наибольшее влияние на закономерность изменения тока оказывает расход раствора. Предварительный анализ показывает, что полное описание плазмоэлектролитического процесса не может базироваться на чисто физических или чисто химических представлениях. Это - взаимосвязанные физико-химические процессы, поэтому разделить их на физические и химические можно лишь условно.
Дата добавления: 2015-04-15; просмотров: 4467;
