Понятие системы искусственного интеллекта (ИИ). Направления использования систем искусственного интеллекта (ИИ). Роль и место систем ИИ в корпоративных информационных системах.
Под Искусственным Интеллектом (ИИ) понимается область исследований, в которой ставится задача изучения и моделирования принципов и механизмов интеллектуальной деятельности человека. Конечной практической целью работ в области ИИ является создание работающих моделей разумного поведения в виде программных или иных технических средств, а также технологий программирования самого такого поведения.
Искусственный интеллект (ИИ) - это наука о концепциях, позволяющих вычислительной машине делать такие вещи, которые у людей выглядят разумными.
Термин «искусственный интеллект» имеет два основных значения:
Во-первых, под ним понимается теория создания программных и аппаратных средств, способных осуществлять интеллектуальную деятельность, сопоставимую с интеллектуальной деятельностью человека.
Во-вторых, сами такие программные аппаратные средства, а также выполняемая с их помощью деятельность.
Система искусственного интеллекта — это набор программных и аппаратных средств, использование которых должно было бы привести к тем же результатом, к которым при решении данного класса задач приводит интеллектуальная деятельность человека.
ИИ включает технологии:
· решения задач, экспертных систем (ЭС), систем поддержки и принятия решений;
· систем распознавания образов, движения и т. д.;
· систем обработки текста и машинного перевода;
· игровых программ. Например, шахматы;
· обучаемых и обучающих систем;
· робототехники и автономных агентов;
· взаимодействия с пользователем на естественном языке.
Предпосылки возникновения
1950 г. – в английском журнале “Mind” выходит статья Тьюринга “Computing Machinery and Intelligence”, в которой предлагается критерий наличия у машины (программы) мыслительных способностей (тест Тьюринга).
Термин artificial intelligence был впервые применен в 1956 году на семинаре в одном из американских вузов.
1962 г. – Розенблатом предложены персептроны – модели мозга в виде различного рода сетей из искусственных нейронов, в основе – модели Маккалока-Питтса (1943 г.).
1965 г. – Дж. Э. Робинсон “Машинно-ориентированная логика, основанная на принципе резолюции”.
1966 г. – впервые было предложено моделирование на ЭВМ процесса эволюции в живой природе. В основе – исследование мутаций и избирательного выживания в течение 2-х млрд. лет.
1970-е гг.– становление логического программирования, в СССР получают развитие логико-математические модели в системах управления. Появилась система автоматизированного перевода документации ЭСПРИТ, разработанная в рамках европейской программы.
Впервые термин «искусственный интеллект» был введен в научную практику летом 1956 г. В это время в Дартмусе (США) по инициативе известного американского специалиста по теории и практике ЭВМ Джона Маккарти проходила научная конференция, на которой присутствовали К. Шеннон, М. Минский, Г. Саймон, А. Ньюэлл и др. Целью конференции было обсудить возможность создания ИИ, что и было отражено в названии конференции — Dartmouth Summer Research Project on Artificial Intelligence.
Участники конференции в своих выступлениях не могли обойти вниманием статью английского математика Алана Тьюринга «Computing machinary and intelligence», опубликованную в 1950 г. и прямо относящуюся к проблематике ИИ (хотя этот термин в ней не использовался). В своей работе А. Тьюринг сформулировал свой знаменитый тест, согласно которому компьютер демонстрирует интеллектуальное поведение в том случае, если он способен действовать так, что наблюдатель не в состоянии решить, имеет ли он дело с компьютером или с человеком.
Как научное направление ИИ тесно связано с философией, психологией, лингвистикой, антропологией, нейронаукой.
Значительным продвижением в развитии теории ИИ было выдвижение идеи М. Мински и Р. Шенка. о фреймах. Фрейм — целостная структура, содержащая информацию об основных свойствах и признаках понятия. Это сетевая конструкция, вершина которой содержит общие признаки, а связи, идущие от этих вершин, позволяют продвигаться к более конкретной информации. Фреймы — это решение задачи представления знаний в компьютерной системе.
Рассматривая становление концепций ИИ, выделяют три этапа. Исследовательским полем для развития методов ИИ на первом этапе явились всевозможные игры, головоломки, математические задачи. Выбор таких задач обуславливался простотой и ясностью проблемы.
Основной расцвет такого рода исследований приходится на конец 1960-х гг., после чего стали появляться попытки применения разработанных методов для задач, решаемых не в искусственных, а в реальных средах. Необходимость исследования систем ИИ при их функционировании в реальном мире привело к постановке задачи создания интегральных роботов. Проведение таких работ и составляет сущность второго этапа исследований. В Стэнфордском университете были разработаны экспериментальные роботы, функционирующие в лабораторных условиях. Проведение этих экспериментов показало необходимость решения вопросов, связанных с проблемой представления знаний, зрительного восприятия, построения сложных планов поведения в динамических средах, общения с роботами на естественном языке.
Эти проблемы были более ясно сформулированы и поставлены перед исследователями в середине 1970-х гг., связанных с началом третьего этапа исследований систем ИИ. Его характерной чертой явилось создание человеко-машинных систем, интегрирующих в единое целое интеллект человека и способности машины для достижения общей цели.
Математические методы и модели искусственного интеллекта: нечеткая логика, генетические алгоритмы, нейронные сети и др. Интеллектуальный анализ данных. Управление знаниями.
В основе нечеткой логики лежит теория нечетких множеств, изложенная в серии работ Л. Заде в 1965-1973 годах. Математическая теория нечетких множеств (fuzzy sets) и нечеткая логика (fuzzy logic) являются обобщениями классической теории множеств и классической формальной логики. Основной причиной появления новой теории стало наличие нечетких и приближенных рассуждений при описании человеком процессов, систем, объектов.
Л. Заде, формулируя это главное свойство нечетких множеств, базировался на трудах предшественников. В начале 1920-х годов польский математик Лукашевич трудился над принципами многозначной математической логики, в которой значениями предикатов могли быть не только «истина» или «ложь». В 1937 году еще один американский ученый М. Блэк впервые применил многозначную логику Лукашевича к спискам как множествам объектов и назвал такие множества неопределенными.
Нечеткая логика как научное направление развивалась непросто, не избежала она и обвинений в лженаучности. Даже в 1989 году, когда примеры успешного применения нечеткой логики в обороне, промышленности и бизнесе исчислялись десятками, Национальное научное общество США обсуждало вопрос об исключении материалов по нечетким множествам из институтских учебников.
Первый период развития нечетких систем (конец 60-х – начало 70-х гг.) характеризуется развитием теоретического аппарата нечетких множеств. В 1970 году Беллман совместно с Заде разработали теорию принятия решений в нечетких условиях.
В 70-80 годы (второй период) появляются первые практические результаты в области нечеткого управления сложными техническими системами (парогенератор с нечетким управлением). И. Мамдани в 1975 году спроектировал первый функционирующий на основе алгебры Заде контроллер, управляющий паровой турбиной. Одновременно стало уделяться внимание вопросам создания экспертных систем, построенных на нечеткой логике, разработке нечетких контроллеров. Нечеткие экспертные системы для поддержки принятия решений нашли широкое применение в медицине и экономике.
Наконец, в третьем периоде, который длится с конца 80-х годов и продолжается в настоящее время, появляются пакеты программ для построения нечетких экспертных систем, а области применения нечеткой логики заметно расширяются. Она применяется в автомобильной, аэрокосмической и транспортной промышленности, в области изделий бытовой техники, в сфере финансов, анализа и принятия управленческих решений и многих других. Кроме того, немалую роль в развитии нечеткой логики сыграло доказательство знаменитой теоремы FAT (Fuzzy Approximation Theorem) Б. Коско, в которой утверждалось, что любую математическую систему можно аппроксимировать системой на основе нечеткой логики.
Информационные системы, базирующиеся на нечетких множествах и нечеткой логике, называют нечеткими системами.
Достоинства нечетких систем:
· функционирование в условиях неопределенности;
· оперирование качественными и количественными данными;
· использование экспертных знаний в управлении;
· построение моделей приближенных рассуждений человека;
· устойчивость при действии на систему всевозможных возмущений.
Недостатками нечетких систем являются:
· отсутствие стандартной методики конструирования нечетких систем;
· невозможность математического анализа нечетких систем существующими методами;
· применение нечеткого подхода по сравнению с вероятностным не приводит к повышению точности вычислений.
Теория нечетких множеств. Главное отличие теории нечетких множеств от классической теории четких множеств состоит в том, что если для четких множеств результатом вычисления характеристической функции могут быть только два значения – 0 или 1, то для нечетких множеств это количество бесконечно, но ограничено диапазоном от нуля до единицы.
Нечеткое множество. Пусть U – так называемое универсальное множество, из элементов которого образованы все остальные множества, рассматриваемые в данном классе задач, например множество всех целых чисел, множество всех гладких функций и т.д. Характеристическая функция множества 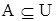 – это функция
– это функция 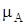 , значения которой указывают, является ли
, значения которой указывают, является ли 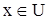 элементом множества A:
элементом множества A:
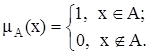
В теории нечетких множеств характеристическая функция называется функцией принадлежности, а ее значение 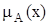 – степенью принадлежности элемента x нечеткому множеству A.
– степенью принадлежности элемента x нечеткому множеству A.
Более строго: нечетким множеством A называется совокупность пар
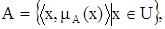
где 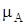 – функция принадлежности, то есть
– функция принадлежности, то есть 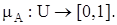
Пусть, например, U ={a, b, c, d, e}, 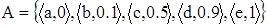 . Тогда элемент a не принадлежит множеству A, элемент b принадлежит ему в малой степени, элемент c более или менее принадлежит, элемент d принадлежит в значительной степени, e является элементом множества A.
. Тогда элемент a не принадлежит множеству A, элемент b принадлежит ему в малой степени, элемент c более или менее принадлежит, элемент d принадлежит в значительной степени, e является элементом множества A.
Пример. Пусть универсум U есть множество действительных чисел. Нечеткое множество A, обозначающее множество чисел, близких к 10, можно задать следующей функцией принадлежности (рис. 21.1):
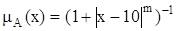 ,
,
где 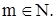
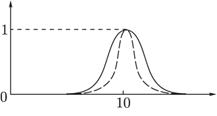
Рис. 21.1. Функция принадлежности 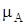
Показатель степени m выбирается в зависимости от степени близости к 10. Например, для описания множества чисел, очень близких к 10, можно положить m = 4, для множества чисел, не очень далеких от 10, m = 1.
Носителем нечеткого множества A называется четкое множество 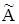 таких точек в U, для которых величина
таких точек в U, для которых величина 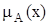 положительна, то есть
положительна, то есть 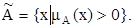
Ядром нечеткого множества A называется четкое множество 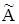 таких точек в U, для которых величина
таких точек в U, для которых величина 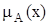 = 1.
= 1.
Множеством уровня 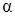 (
( 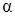 -срезом) нечеткого множества A называется четкое подмножество универсального множества U, определяемое по формуле
-срезом) нечеткого множества A называется четкое подмножество универсального множества U, определяемое по формуле 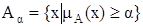 , где
, где 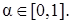
Функцию принадлежности называют нормальной, если ядро нечеткого множества содержит хотя бы один элемент.
Операции над нечеткими множествами. Для нечетких множеств, как и для обычных, определены основные операции: объединение, пересечение и инверсия/дополнение.
Для определения пересечения и объединения нечетких множеств наибольшей популярностью пользуются следующие три группы операций:
| Максиминные | 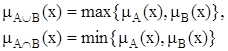
|
| Алгебраические | 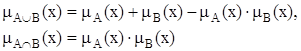
|
| Ограниченные | 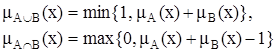
|
Дополнение нечеткого множества во всех трех случаях определяется одинаково:
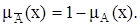
При максиминном и алгебраическом определении операций не будут выполняться законы противоречия и исключения третьего:
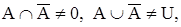
а в случае ограниченных операций не будут выполняться свойства идемпотентности и дистрибутивности:
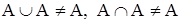 ,
,
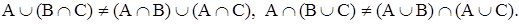
Можно показать, что при любом построении операций объединения и пересечения в теории нечетких множеств приходится отбрасывать либо законы противоречия и исключения третьего, либо законы идемпотентности и дистрибутивности.
Нечеткая логика. Понятие нечеткой и лингвистической переменных используется при описании объектов и явлений с помощью нечетких множеств.
Нечеткая переменная характеризуется тройкой <b, X, A>, где b – наименование переменной, X – универсальное множество (область определения b), A – нечеткое множество на X, описывающее ограничения (то есть b A(x)) на значения нечеткой переменной a.
Лингвистической переменной называется набор <b, T, X, G, M>, где b – наименование лингвистической переменной, Т – множество ее значений (терм-множество), представляющих собой наименования нечетких переменных, областью определения каждой из которых является множество X (множество T называется базовым терм-множеством лингвистической переменной), G – синтаксическая процедура, позволяющая оперировать элементами терм-множества T, в частности генерировать новые термы (значения), М – семантическая процедура, позволяющая превратить каждое новое значение лингвистической переменной, образуемое процедурой G, в нечеткую переменную, то есть сформировать соответствующее нечеткое множество.
Лингвистическую переменную можно определить как переменную, значениями которой являются не числа, а слова или предложения естественного (или формального) языка. Например, лингвистическая переменная «возраст» может принимать следующие значения: «очень молодой», «молодой», «среднего возраста», «старый», «очень старый» и др. Ясно, что переменная «возраст» будет обычной переменной, если ее значения – точные числа; лингвистической она становится, будучи использованной в нечетких рассуждениях человека.
Каждому значению лингвистической переменной соответствует определенное нечеткое множество со своей функцией принадлежности. Так, лингвистическому значению «молодой» может соответствовать функция принадлежности, изображенная на рисунке 21.2.
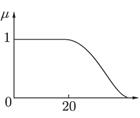
Рис. 21.2. Функция принадлежности значения «молодой» лингвистической переменной «возраст»
Основой для проведения операции нечеткого логического вывода является база правил, содержащая нечеткие высказывания в форме «если…, то…» и функции принадлежности для соответствующих лингвистических термов. При этом должны соблюдаться следующие условия:
существует хотя бы одно правило для каждого лингвистического терма выходной переменной;
для любого терма входной переменной имеется хотя бы одно правило, в котором этот терм используется в качестве предпосылки (левая часть правила).
В противном случае имеет место неполная база нечетких правил. Для реализации логического вывода необходимо выполнить следующее:
· Сопоставить факты с каждым из правил и определить степень соответствия, назначив текущую силой правил;
· Для каждого правила, сила которого больше заданного порога, вычислить достоверность левой части;
· Для каждого правила с помощью оператора импликации вычислить достоверность правой части;
· Для многих результатов, полученных по различным правилам, выбрать одно (усредненное).
Нейронные сети (НС) – очень мощный метод моделирования, позволяющий воспроизводить чрезвычайно сложные зависимости, нелинейные по свой природе. Как правило, нейронная сеть используется тогда, когда неизвестны предположения о виде связей между входами и выходами (хотя, конечно, от пользователя требуется какой-то набор эвристических знаний о том, как следует отбирать и подготавливать данные, выбирать нужную архитектуру сети и интерпретировать результаты).
На вход нейронной сети подаются представительные данные и запускается алгоритм обучения, который автоматически анализирует структуру данных и генерирует зависимость между входом и выходом. Для обучения НС применяются алгоритмы двух типов: управляемое («обучение с учителем») и неуправляемое («без учителя»).
Простейшая сеть имеет структуру многослойного персептрона с прямой передачей сигнала (рис. 21.3), которая характеризуется наиболее устойчивым поведением. Входной слой служит для ввода значений исходных переменных, затем последовательно отрабатывают нейроны промежуточных и выходного слоев. Каждый из скрытых и выходных нейронов, как правило, соединен со всеми элементами предыдущего слоя (для большинства вариантов сети полная система связей является предпочтительной). В узлах сети активный нейрон вычисляет свое значение активации, беря взвешенную сумму выходов элементов предыдущего слоя и вычитая из нее пороговое значение. Затем значение активации преобразуется с помощью функции активации (или передаточной функции), и в результате получается выход нейрона. После того, как вся сеть отработает, выходные значения элементов последнего слоя принимаются за выход всей сети в целом.
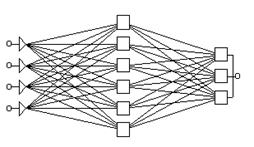
Рис. 21.3. Пример нейронной сети – трехслойного персептрона с прямым распространением информации
Наряду с моделью многослойного персептрона, позднее возникли и другие модели нейронных сетей, различающихся по строению отдельных нейронов, по топологии связей между ними и по алгоритмам обучения. Среди наиболее известных сейчас вариантов можно назвать НС с обратным распространением ошибки, основанные на радиальных базисных функциях, обобщенно-регрессионные сети, НС Хопфилда и Хэмминга, самоорганизующиеся карты Кохонена, стохастические нейронные сети и т.д. Существуют работы по рекуррентным сетям (т.е. содержащим обратные связи, ведущие назад от более дальних к более ближним нейронам), которые могут иметь очень сложную динамику поведения. Начинают эффективно использоваться самоорганизующиеся (растущие или эволюционирующие) нейронные сети, которые во многих случаях оказываются более предпочтительными, чем традиционные полносвязные НС.
Для моделей, построенных по мотивам человеческого мозга, характерны, как легкое распараллеливание алгоритмов и связанная с этим высокая производительность, так и не слишком большая выразительность представленных результатов, не способствующая извлечению новых знаний о моделируемой среде. Попытаться в явном виде представить результаты нейросетевого моделирования – довольно неблагодарная задача. Поэтому основной удел этих моделей, являющихся своеобразной "вещью в себе", – прогнозирование.
Важным условием применения НС, как и любых статистических методов, является объективно существующая связь между известными входными значениями и неизвестным откликом. Эта связь может носить случайный характер, искажена шумом, но она должна существовать. Известный афоризм “garbage in, garbage out” (“мусор на входе – мусор на выходе”) нигде не справедлив в такой степени, как при использовании методов нейросетевого моделирования. Это объясняется, во-первых, тем, чтоитерационные алгоритмы направленного перебора комбинаций параметров нейросети оказываются весьма эффективными и очень быстрыми лишь при хорошем качестве исходных данных. Однако, если это условие не соблюдается, число итераций быстро растет и вычислительная сложность оказывается сопоставимой с экспоненциальной сложностью алгоритмов полного перебора возможных состояний. Во-вторых, сеть склонна обучаться прежде всего тому, чему проще всего обучиться, а, в условиях сильной неопределенности и зашумленности признаков, это – прежде всего артефакты и явления "ложной корреляции".
Искусственные нейронные сети (ИНС) — математические модели, а также их программные или аппаратные реализации, построенные по принципу организации и функционирования биологических нейронных сетей — сетей нервных клеток живого организма. Это понятие возникло при изучении процессов, протекающих в мозге, и при попытке смоделировать эти процессы. Первой такой попыткой были нейронные сети Маккалока и Питтса. Впоследствии, после разработки алгоритмов обучения, получаемые модели стали использовать в практических целях: в задачах прогнозирования, для распознавания образов, в задачах управления и др.
Генетические алгоритмы. «Отцом» генетических алгоритмов по праву считается Д. Холланд, метод вначале назывался репродуктивным планом Холланда. В дальнейшем генетические алгоритмы развивались в работах учеников Холланда: Д. Голдберга и К. Де Йонга – именно в них и закрепилось название метода.
Генетические алгоритмы – это раздел эволюционного моделирования, заимствующий методические приемы из теоретических положений генетики.
Генетические алгоритмы – адаптивные методы поиска, которые используются для решения задач функциональной оптимизации. Представляют собой своего рода модели машинного исследования поискового пространства, построенные на эволюционной метафоре. Характерные особенности: использование строк фиксированной длины для представления генетической информации, работа с популяцией строк, использование генетических операторов для формирования будущих поколений.
Генетические алгоритмы применяются для решения следующих задач:
· оптимизация функций;
· разнообразные задачи на графах (задача коммивояжера и т.д.);
· настройка и обучение искусственной нейронной сети;
· задачи компоновки;
· составление расписаний;
· игровые стратегии;
· аппроксимация функций;
· искусственная жизнь;
· биоинформатика.
Преимущества генетических алгоритмов: универсальность, высокая обзорность поиска, нет ограничений на целевую функцию, любой способ задания функции.
Недостатки генетических алгоритмов: относительно высокая вычислительная стоимость и квазиоптимальность.
Когда надо использовать генетический алгоритм: много параметров, плохая целевая функция, комбинаторные задачи.
Когда не надо использовать генетический алгоритм: задача хорошо решается традиционными методами, требуется высокая точность решения.
Понятие системы поддержки принятия решений (СППР). Классификация ССПР. Архитектура и принципы построения СППР.
Функциональная структура использования СИИ. Эта структура состоит из трех комплексов вычислительных средств (рис.21.4). Первый комплекс представляет собой совокупность средств, выполняющих программы (исполнительную систему), спроектированных с позиций эффективного решения задач, имеет в ряде случаев проблемную ориентацию. Второй комплекс - совокупность средств интеллектуального интерфейса, имеющих гибкую структуру, которая обеспечивает возможность адаптации в широком спектре интересов конечных пользователей. Третьим комплексом средств, с помощью которых организуется взаимодействие первых двух, является база знаний, обеспечивающая использование вычислительными средствами первых двух комплексов целостной и независимой от обрабатывающих программ системы знаний о проблемной среде. Исполнительная система (ИС) объединяет всю совокупность средств, обеспечивающих выполнение сформированной программы. Интеллектуальный интерфейс - система программных и аппаратных средств, обеспечивающих для конечного пользователя использование компьютера для решения задач, которые возникают в среде его профессиональной деятельности либо без посредников либо с незначительной их помощью. База знаний (БЗ) - занимает центральное положение по отношению к остальным компонентам вычислительной системы в целом, через БЗ осуществляется интеграция средств ВС, участвующих в решении задач.
Система поддержки принятия решений - диалоговая автоматизированная информационная система, использующая правила принятия решений и соответствующие модели с базами данных, а также интерактивный компьютерный процесс моделирования, поддерживающий принятие самостоятельных и неструктурированных решений отдельными менеджерами и личным опытом лица, принимающего решения, для получения конкретных, реализуемых решений проблем, не поддающихся решению обычными методами. Системы поддержки принятия решений - это одна из важнейших категорий информационных систем управления.
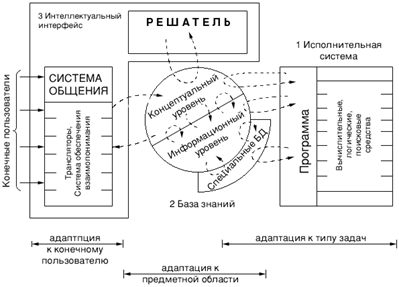
Рис. 21.4. Функциональная структура СИИ
Система поддержки принятия решений – это компьютерная система, помогающая пользователю решать проблемы повседневной профессиональной деятельности на основе использования баз данных, баз знаний, баз моделей, путём предоставления выводов, рекомендаций оценок возможных альтернативных вариантов решения проблемы. То есть СППР помогает пользователю решить сложную задачу в автоматизированном режиме.
СППР позволяют преодолеть трудности, связанные с многокритериальностью при решении задачи, ограниченностью ресурсов, неполнотой информации. Данные системы предполагают сочетание логического мышления, интуиции пользователя, с математическими методами и возможностями ЭВМ. Архитектура СППР приведена на рисунке 21.5.
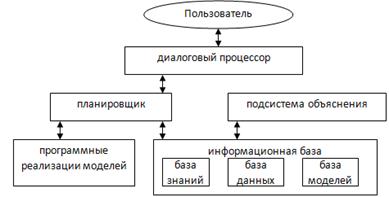
Рис. 21.5. Архитектура СППР
В последнее время СППР начинают применяться и в интересах малого и среднего бизнеса (например, выбор варианта размещения торговых точек, выбор кандидатуры на замещение вакантной должности, выбор варианта информатизации и т. д.). В общем, они способны поддержать индивидуальный стиль и соответствовать персональным потребностям менеджера.
Существуют системы, созданные для решения сложных проблем в больших коммерческих и государственных организациях.
Когда классифицируют СППР, учитывают:
структурированность решаемых управленческих задач;
уровень иерархии управления фирмой, на котором решение должно быть принято;
принадлежность решаемой задачи к той или иной функциональной сфере бизнеса;
вид используемой информационной технологии.
На техническом уровне различает СППР всего предприятия и настольную СППР. СППР всего предприятия подключена к большим хранилищам информации и обслуживает многих менеджеров предприятия. Настольная СППР – это малая система, обслуживающая лишь один компьютер пользователя.
В зависимости от данных, с которыми эти системы работают, СППР условно можно разделить на оперативные и стратегические. Оперативные СППР предназначены для немедленного реагирования на изменения текущей ситуации в управлении финансово-хозяйственными процессами компании. Стратегические СППР ориентированы на анализ значительных объемов разнородной информации, собираемых из различных источников.
Целесообразно определить три класса СППР в зависимости от сложности решаемых задач и областей применения.
СППР первого класса, обладающие наибольшими функциональными возможностями, предназначены для применения в органах государственного управления высшего уровня (администрация президента, министерства) и органах управления больших компаний (совет директоров корпорации) при планировании крупных комплексных целевых программ для обоснования решений относительно включения в программу различных политических, социальных или экономических мероприятий и распределения между ними ресурсов на основе оценки их влияния на достижение основной цели программы. СППР этого класса являются системами коллективного пользования, базы данных которых формируются многими экспертами - специалистами в различных областях знаний.
СППР второго класса являются системами индивидуального пользования, базы данных которых формируются непосредственным пользователем. Они предназначены для использования государственными служащими среднего ранга, а также руководителями малых и средних фирм для решения оперативных задач управления.
СППР третьего класса являются системами индивидуального пользования, адаптирующимися к опыту пользователя. Они предназначены для решения часто встречающихся прикладных задач системного анализа и управления (например, выбор субъекта кредитования, выбор исполнителя работы, назначение на должность). Такие системы обеспечивают получение решения текущей задачи на основе информации о результатах практического использования решений этой же задачи, принятых в прошлом.
Особенности многокритериальных задач принятия решений. Основные понятия метода анализа иерархий. Информационно-аналитические СППР, основанные на анализе иерархических процессов.
Основная идея метода анализа иерархий.
Решение многокритериального выбора путём:
· Представления системы критериев (целей) в виде иерархической структуры.
· Оценки приоритетов (весов) критериев с учётом их места в иерархии относительной важности.
· Определения лучшей альтернативы по значениям её характеристик и важности критериев.
Основное назначение метода – решение задач многокритериальных слабоструктурированных задач принятия решений.
Иерархия: многоуровневая структура, в которой вышестоящие вершины доминируют над нижестоящими.
Преимущества иерархии как средства описания задачи:
Процесс построения иерархии исходит из способа мышления человека.
Иерархическое представление задачи принятия решения позволяет описывать влияние элементов одного уровня на элементы другого уровня (рис. 21.6).
Иерархия устойчива и гибка в том смысле, что малые её изменения (удаление и добавление элементов) не разрушают характеристик иерархии.
Основные этапы решения задачи методом анализа иерархий:
Структуризация задачи принятия решения в виде иерархии с несколькими уровнями: цели-критерии-альтернативы;
Проведение попарного сравнения элементов иерархии, преобразование результатов сравнения в числа;
Вычисление коэффициентов важности элементов каждого уровня. Проверка согласованности суждений ЛПР;
Подсчёт количественного индикатора качества альтернатив и определение наилучшей альтернативы.
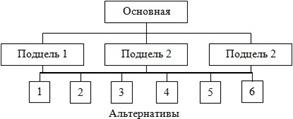
Рис. 21.6. Графическое представление МАИ
Попарное сравнение элементов иерархии:
Элементы сравниваются попарно по отношению к их воздействию на общую для них характеристику. Результаты парного сравнения представляются в виде квадратной матрицы парных сравнений.
Элементы матрицы парных сравнений – числа, характеризующие относительную важность элементов по отношению к общей для них характеристике. Матрицы парных сравнений заполняются ЛПР (экспертом).
Матрицы парных сравнений (рис. 21.7) строятся для критериев (по степени их влияния на достижение цели) и для альтернатив (по степени их влияния на критерии).
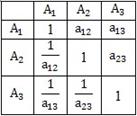
Рис. 21.7. Матрица парных сравнений
Матрица парных сравнений – обратно симметричная. Диагональ состоит из единиц. Элементы матрицы 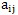 определяются по шкале относительной важности (табл. 21.1).
определяются по шкале относительной важности (табл. 21.1).
Таблица 21.1
Шкала субъективных суждений
| Значения | Определение |
| Значение не существенно | |
| Небольшое значение | |
| Большое значение | |
| Значительное значение | |
| Максимальное значение | |
| 2, 4, 6, 8 | Промежуточные значения между двумя смежными суждениями |
Информационно-аналитические СППР, основанные на анализе иерархических процессов. Обзор СППР основанных на анализе иерархических процессов представлен в таблице 21.2.
Таблица 21.2
Сводная таблица систем поддержки принятия решений
| Наименование СППР | Официальный сайт системы | Характеристика |
| А | ||
| Super Decisions | http://www. superdecisions.com | Программный продукт, разработанный на основе метода аналитических сетей (Analytic Network Process) |
| Expert Choice | http://www. expertchoice.com | Коммерческий программный продукт, разработанный на основе метода анализа иерархий для поддержки принятия решений различным организациям. Система имеет три варианта поставки: Comparion Core™, Expert Choice 11.5™ и Expert Choice Inside |
| Imaginatik Idea Central | http://www. imaginatik.com | Коммерческая система, являющаяся веб-приложением для обработки мнений экспертов |
| ELECTRE IS | http://www. lamsade. dauphine.fr/ enlish/ software. html | Система, основанная на многокритериальном методе из семейства ELECTRE, который позволяет использовать псевдокритерии и пороговые значения при принятии решений. В процессе вычислений система строит граф. Искомый набор альтернатив - это ядро этого графа |
| IRIS | http://www4.fe.uc.pt/ lmcdias/ iris.htm | Система реализует задачу сортировки альтернатив в многокритериальных задачах принятия решений. Допускает задание пороговых ограничений пользователем для критериев (признаков). Способна оценивать точность вычислений. Выводит результат вычислений в виде отчета |
| Император 3.1 | http://www. neirosplav.com | Возможности программы позволяют решать задачи рейтингования, выбора альтернатив, распределения ресурсов, прогнозирования, планирования, учета предпочтений, моделирования ситуаций. В основу системы поддержки принятия решения "Император" положен метод анализа иерархий |
Проектирование экспертной системы с использованием программы EXSYS Rule Book.
Дата добавления: 2015-04-10; просмотров: 6037;
