ПРИМЕР РЕШЕНИЯ ЗАДАЧИ ОПТИМАЛЬНОГО РАЗМЕЩЕНИЯ ВЦ И АП НА ТЕРРИТОРИИ РЕГИОНА С ЗАДАННОЙ ПЛОЩАДЬЮ
Пример решения указанной задачи представим с численными значениями, чтобы оценить полученные в результате расчетов величины.
Исходными данными для расчета являются:
- D,L - ширина и длина региона, определяемая согласно площади региона ( 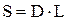 ).
).
- Принимаем D=10, L=8 км;
- N=8000 – число абонентов сети;
- 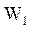 =350 - капитальные затраты на установку одного ВЦ, тыс. грн.;
=350 - капитальные затраты на установку одного ВЦ, тыс. грн.;
- 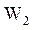 =15 - капитальные затраты на установку одного АП, тыс. грн.;
=15 - капитальные затраты на установку одного АП, тыс. грн.;
- 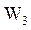 =20 - стоимость 1 км канала связи между ВЦ,
=20 - стоимость 1 км канала связи между ВЦ, 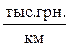 ;
;
- 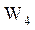 =10 - стоимость 1 км канала связи между АП и ВЦ,
=10 - стоимость 1 км канала связи между АП и ВЦ,  ;
;
- 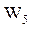 =5 - удельные затраты на передачу объема информации на единицу длины канала связи между ВЦ,
=5 - удельные затраты на передачу объема информации на единицу длины канала связи между ВЦ,  ;
;
- WS = 15000 - суммарные расходы на производство и обслуживание сети, тыс.грн.
Приняты обозначения: ВЦ – вычислительный центр, АП – абонентский пункт.
Решение.
1. Дадим рекомендации по выбору технических средств проектируемой информационной сети.
Определимся, что задана коммуникационная сеть с каналами средней удаленности и равномерным распределением затрат.На основании анализа начальных условий проектирования выбирается один из возможных вариантов исходной топологической структуры или стоимостной класс сети (рис. 1). Для неё составляются соответствующие расчетные соотношения. Так как задана коммуникационная сеть с каналами средней удаленности и равномерным распределением затрат, то этому случаю соответствует класс с индексами 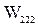 . Общее выражение для полных затрат, включая затраты на создание сети, эксплуатационные расходы для любой ИС данного класса
. Общее выражение для полных затрат, включая затраты на создание сети, эксплуатационные расходы для любой ИС данного класса 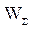 имеет вид:
имеет вид:
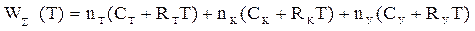 ,
,
где 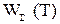 - полные суммарные затраты на создание сети и обслуживание ее функционирования в течение времени
- полные суммарные затраты на создание сети и обслуживание ее функционирования в течение времени 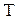 ;
; 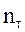 ,
, 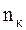 ,
, 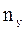 - число в сети терминалов, каналов и узлов соответственно;
- число в сети терминалов, каналов и узлов соответственно; 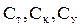 - начальная стоимость одного терминала, канала и узла соответственно;
- начальная стоимость одного терминала, канала и узла соответственно;  - расходы денежных средств в единицу времени на эксплуатацию терминала, канала и узла соответственно;
- расходы денежных средств в единицу времени на эксплуатацию терминала, канала и узла соответственно; 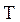 - срок действия сети с начала функционирования.
- срок действия сети с начала функционирования.
Для сети с равномерно распределенным стоимостным классом 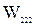 из него вытекает ряд следующих соотношений:
из него вытекает ряд следующих соотношений:
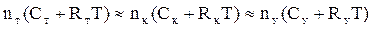 ,
,
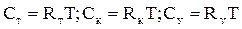 ,
,
откуда выражение суммарных затрат:
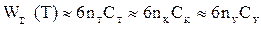 .
.
Далее процесс проектирования продолжается выбором исходного варианта топологической структуры ИС, терминалов 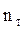 , каналов связи и оборудования сетевых узлов, стоимость которых известна и последующий проверочный расчет в соответствии с полученными соотношениями.
, каналов связи и оборудования сетевых узлов, стоимость которых известна и последующий проверочный расчет в соответствии с полученными соотношениями.
Если стоимостные логические условия выполняется, то можно остановиться на сделанном выборе; если нет, то решение должно быть пересмотрено, т. е. должны быть изменены либо стоимость терминала, каналов связи и оборудования сетевых узлов, либо их число.
2. Решение задачи оптимального размещения узлов сети.
Введём ряд допущений, которые позволят получить решение в аналитическом виде - пользователи размещены по территории региона с равной плотностью; запросы пользователей однородны, а их поток имеет постоянную интенсивность во времени; преобразование, сбор и промежуточное хранение информации осуществляются в ВЦ и АП; потребители с АП и ВЦ связаны радиально.
Общая схема размещения ВЦ в сети представлена на рис. 2, где окружностями обозначены зоны действия каждого ВЦ.
Поиск R производится следующим образом: на большом интервале с заданным шагом берутся точки (значения R). Производится подстановка R в выражение минимизации затрат:
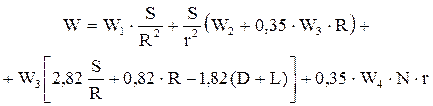 .
.
Находим частные производные от полных затрат W по переменным R и r с целью определения экстремальных значений этих величин для функции W и прировняв их нулю, решаем совместно полученные уравнения. Определяем корни полученного алгебраического уравнения. Для заданных значений коэффициентов найдем множество значений корней 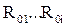 . Из этого множества, естественно, исключаются элементы, определяющие мнимые и отрицательные значения, остальные проверяются на соответствие физическому смыслу задачи.
. Из этого множества, естественно, исключаются элементы, определяющие мнимые и отрицательные значения, остальные проверяются на соответствие физическому смыслу задачи.
Полученные значения затрат сортируются по возрастанию, наименьшие значения выводятся в списке найденных значений. Произведя вычисления, например, при помощи программы MathCad, получаем массив значений:
R={5,120 5,200 5,280 5,360 5,440 5,520 5,600 5,680 0,960 5,760 …}.
Выбрав одно из наиболее подходящих значений R=5,12 км, находим далее соответствующие этому значению величины, определяющие оптимальное распределение затрат для синтезируемой сети:
- 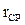 - среднее расстояние между АП и ВЦ:
- среднее расстояние между АП и ВЦ:
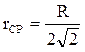 =1.81 км;
=1.81 км;
- 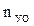 - оптимальное число узлов (ВЦ):
- оптимальное число узлов (ВЦ):
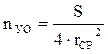 =7;
=7;
-  - среднее число АП, подсоединенных к каждому узлу:
- среднее число АП, подсоединенных к каждому узлу:
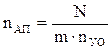 =23,
=23,
где 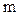 =N/(nyo nАП)=50 - среднее число абонентов на 1 АП.
=N/(nyo nАП)=50 - среднее число абонентов на 1 АП.
После расчета основных параметров необходимо приступить к синтезу топологии ИС (рис 5).
Для топологического проектирования из перечисленных параметров наиболее важным является оптимальное число узлов в сети. В тех случаях, когда стоимость является главным критерием, синтез топологической структуры может быть проведен по минимуму этого критерия.
При решении поставленной задачи можно для пунктов расположения абонентов построить минимальное покрывающее дерево, обеспечивающее минимальное значение суммарной длины линий передачи сообщений между ВЦ, для этого применяется, как правило, алгоритм Литтла [1]. В некоторых случаях, когда задана исходная матрица расстояний, она может быть принята в качестве весовых значений дуг.
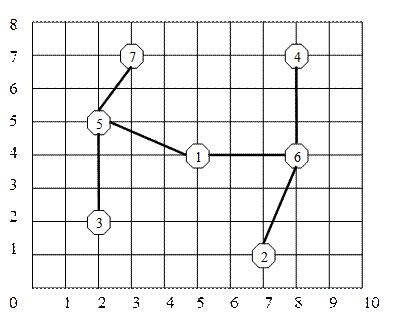
Рисунок 5 - Синтез топологии ИС
Координаты ВЦ согласно полученной топологической структуре сети сводим в таблицу (табл. 3).
Таблица 3 - Координаты ВЦ
| Номер ВЦ | Х, км | Y, км |
3. Проведем простейший топологический анализ полученной сети.
При анализе сетевых топологических структур выделяют особенности их построения, характеризующие функционирование сети: определяют центральный узел сети и оптимально размещают коммутационные узлы.
Центр сети должен располагаться в таком узле, от которого сумма значений путей до всех остальных (коммутационных) была бы минимальной. Определив «вершину» сети, определяем функции узлов в рамках полученной топологии сети – определяем так называемые полярные пары типа «периферия-центр», «управляющий-подчиненный». Это позволяет рассматривать направления обмена данными, находить максимальные значения потоков и их распределение в принятой топологии сети.
Достижение цели топологического анализа осуществляется решением задачи о максимальном потоке (достижение максимально возможной эффективности связи).
Выделим функции узлов в рамках принятой топологии, как показано на рис.6 и определим объем обрабатываемых запросов (исходное распределение потоков по дугам сети) или объем информационно-вычислительных работ, выполняемых каждым ВЦ для группы 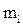 абонентов, принадлежащих к зоне i-го ВЦ. Если определить принадлежность запросов к зоне действия ВЦ следующим образом:
абонентов, принадлежащих к зоне i-го ВЦ. Если определить принадлежность запросов к зоне действия ВЦ следующим образом:
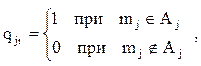
где 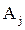 - подмножество абонентов, принадлежащих зоне i-го ВЦ, то объем запросов, поступающих в ВЦ из зоны его действия, составит
- подмножество абонентов, принадлежащих зоне i-го ВЦ, то объем запросов, поступающих в ВЦ из зоны его действия, составит
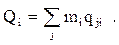
Тогда, согласно принятой топологии сети и проведенным ранее расчетам, получим: Q1=50; Q2=50; Q3=100; Q4=50; Q5=150; Q6=50; Q7=150.
Очевидно, что значение mi в данном случае приобретает смысловую нагрузку минимальной пропускной способности дуги (канала).
Найдем максимальный поток для нашего графа (см. рис. 6), на котором числа, указанные рядом с дугами, обозначают их минимальные пропускные способности, равные в нашем случае mi. Поочередно будем выделять направленные пути графа, ведущие от периферии (самого удаленного узла) к центру.
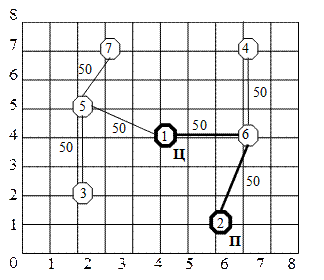
Ц – центр, П – периферия
Рисунок 6 - Функции узлов проектируемой сети
В данном случае существует только один направленный путь, помеченный жирной линией. Тогда, минимальная пропускная способность M разреза П-Ц равна:
МП-Ц = m2-6 + m6-1 = 100.
Это и соответствует максимальному потоку.
4. Проведем функционально-стоимостной анализ сети.
После получения топологии сети необходимо рассчитать оптимальные затраты на установку сети в регионе и ее функционирование. За критерий оптимизации принимаем приведенные затраты на создание и функционирование сети 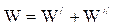 , где
, где 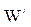 - затраты на производство сети, а
- затраты на производство сети, а 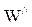 - затраты на ее функционирование.
- затраты на ее функционирование.
Для этого строятся вспомогательные матрицы: матрица смежности |Cм| и матрица расстояний |R|.
Матрица смежности заполняется по следующим соображениям:
- 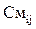 = 0, если нет связи между узлами i и j;
= 0, если нет связи между узлами i и j;
- 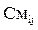 = 1, если есть связь между узлами i и j;
= 1, если есть связь между узлами i и j;
- 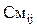 = «-», если i = j.
= «-», если i = j.
Матрица смежности |Cм|:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |||
| 1 | - | ||||||||
| 2 | - | ||||||||
| 3 | - |
| |||||||
| 4 | - | ||||||||
| 5 | - | ||||||||
| 6 | - | ||||||||
| 7 | - |
Матрица |R| показывает относительное расстояние между узлами и заполняется по следующим соображениям:
- 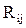 = 0, если нет связи между узлами i и j;
= 0, если нет связи между узлами i и j;
- 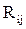 =
= 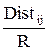 , если есть связь между узлами i и j,
, если есть связь между узлами i и j,
где 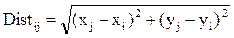 - расстояние между узлами i и j;
- расстояние между узлами i и j;
- 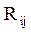 = «-», если i = j.
= «-», если i = j.
Матрица расстояний |R|:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |||
| 1 | - | 0,62 | 0,70 | ||||||
| 2 | - | 0,62 | |||||||
| 3 | - | 0,44 |
| ||||||
| 4 | - | 0,59 | |||||||
| 5 | 0,62 | 0,44 | - | 0,44 | |||||
| 6 | 0,70 | 0,62 | 0,59 | - | |||||
| 7 | 0,44 | - |
Результирующие расходы W/ получаются как сумма капитальных затрат на установку АП и ВЦ, и капитальных затрат на прокладку каналов связи
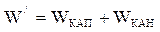 , где:
, где:
- затраты на установку АП и ВЦ:
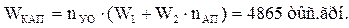 ;
;
- затраты на проведение каналов связи:
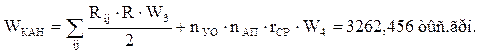 .
.
Следовательно,
W/ = 4865+3262,456=8127,456 тыс.грн.
Определим расходы на функционирование сети 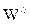 .
.
Расстояние между 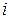 -м и
-м и 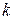 -м ВЦ обозначим
-м ВЦ обозначим 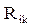 , через
, через 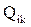 - среднее значение объема информации, циркулирующей между ВЦ с номерами
- среднее значение объема информации, циркулирующей между ВЦ с номерами 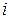 и
и 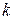 , а через
, а через 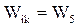 - удельные затраты на передачу объема информации на единицу длины канала связи между этими ВЦ. Рассматриваемая задача относится к числу оптимизационных задач с детерминированными переменными, то есть необходимо минимизировать затраты
- удельные затраты на передачу объема информации на единицу длины канала связи между этими ВЦ. Рассматриваемая задача относится к числу оптимизационных задач с детерминированными переменными, то есть необходимо минимизировать затраты
 .
.
Очевидно, что расстояния между ВЦ будут определены из матрицы расстояний |R|, удельные затраты W5 заданы, а среднее значение объема информации, циркулирующей между ВЦ, определяется объемом запросов, поступающих в ВЦ из зоны его действия - Qi и было рассчитано ранее, тогда:

Тогда, приведенные затраты на создание и функционирование сети будут:
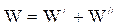 =8127.456+4047.5=12174.956 тыс.грн.
=8127.456+4047.5=12174.956 тыс.грн.
Вывод. По условию, суммарные расходы не должны превышать WS = 15000 тыс.грн. Очевидно, что суммарные расходы не превышают расчетные на производство и обеспечение функционирования сети:
WS > W,
15000>12174.956,
следовательно, выбор оборудования и расчеты проведены корректно.
Дата добавления: 2015-04-10; просмотров: 1040;
