Параметрические модели абстрактных, конкретных и ассоциированных паттерновых сетей

В моделировании компьютерных модульных систем особую роль играют ориентированные паттерновые сети. В этой связи ниже на основе параметрического вектора признаков ориентированных образующих (1) построена параметрическая модель, представляющая абстрактные, конкретные и ассоциированные ориентированных паттерновых сетей.

Сначала будет построена параметрическая модель абстрактных и конкретных ориентированных паттерновых сетей. Затем на основе модели конкретных сетей будет построена параметрическая модель ассоциированных ориентированных сетей.

Итак построим параметрическую модель абстрактных и конкретных ориентированных паттерновых сетей.

Состав абстрактной или конкретной ориентированной паттерновой сети задается набором из n не ассоциированных с данными векторов компонент ориентированных образующих g ,g,...,g , каждый из которых определяется рассмотренным выше вектором (1):

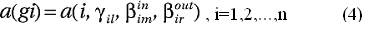
Обратите внимание, что если в соотношении (1) символ i являлся константой, то в соотношениях (4) он принимает значения от 1 до n.

Для каждой i-ой образующей из n образующих, определяемых соотношениями (4), числовые значения ее параметров li,mi,ri выбираются в диапазонах: li=1,2,...; mi=0,1,2,...; ri=0,1,2,..., таким образом, чтобы каждая i-тая образующая представляла один из n реальных модулей, соединенных в систему, моделируемую паттерновой сетью.

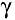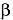Всем переменным и , фигурирующим в векторе (1), ставятся в соответствие домены

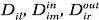(5)

Если в доменах (5) находятся только символы 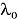, то вектора компонент (4) определяют составы абстрактные паттерновые сети. Если в доменах (5) помимо символов 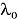находятся данные об одной или нескольких реальных модульных системах. то соотношения (4) определяют составы конкретных паттерновых сетей.

Вектора (4) и домены (5) являются параметрическим "образом" составов многих абстрактных и конкретных паттерновых сетей.

Соотношения (4), (5) определяют наборы образующих, т.е. составы сетей. Чтобы построить параметрическую модель абстрактных и конкретных паттерновых сетей соотношения (4), (5) дополняются набором связок, каждая из которых состоит из двух связей образующих. Набор таких связок называется структурой паттерновой сети.

Структура абстрактной или конкретной ориентированной паттерновой сети в общем случае определяется набором всех ее связок, на каждой из которых установлено отношение связей -соединено, всегда имеющее значение ИСТИНА:

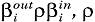-соединено ИСТИНА (6)

Структура паттерновой сети обозначается символом 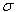, а число связок сети - символом N.

Каждая связка в наборе связок (6) представлена двумя неассоциированными с данными переменными 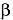, первая из которых принадлежит выходной связи одной образующей, а вторая - входной связи другой образующей.

Символ 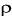называется отношением двух связей, или просто отношением связей. Он присутствует в каждой связке паттерновой сети.

Состав абстрактной паттерновой сети и ее структура называются формой (скелетом) паттерновой сети. Данные, помещенные в доменах конкретной паттерновой сети, являются содержанием сети. Если не все связи сети соединены в связки, то паттерновая сеть имеет не только структуру, определяемую набором связок сети, но также внешние связи, не соединенные в связки и остающиеся свободными. Набор внешних связей паттерновой сети называется внешней структурой сети. Внешние связи сети могут соединяться с внешними связями других паттерновых сетей. Паттерновыми сетями, не имеющими внешних связей, моделируются закрытые модульные системы. Паттерновыми сетями с внешними связями моделируются открытые модульные системы.

На каждой связке абстрактной или конкретной паттерновой сети отношение связей -соединено имеет единственное значение ИСТИНА. Таким образом, все связки любой абстрактной или конкретной паттерновой сети всегда соединены по определению.

На основе соотношений (4), (5), (6), определяющих параметрическую модель конкретных ориентированных паттерновых сетей, несложно построить параметрическую модель ассоциированных ориентированных паттерновых сетей. Для этого необходимо всем переменным 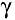и 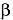, фигурирующим в векторах признаков (4) и в связках (6) присвоить взятые из доменов (5) конкретные данные, характеризующие реальную модульную систему. В результате набор абстрактных векторов признаков образующих (4) превратится в набор ассоциированных векторов признаков образующих, т. е. таких образующих всем, переменным 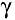и 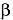которых присвоены конкретные данные об одной реальной модульной системе, взятые из доменов (5).

В результате присвоения данных переменным 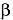, фигурирующим в абстрактных связках (6), получается следующий набор ассоциированных связок:

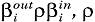-соединено ИСТИНА или ЛОЖЬ (6')

Если все связки абстрактных и конкретных паттерновых сетей всегда являются истинными, то, каждая связка ассоциированной паттерновой сети может находиться в двух состояниях - истинном (соединенном) или ложном (разъединенном).

Будет ли значение отношения связей 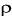-соединено ассоциированной связки сети истинным или ложным зависит от данных, присвоенных ее переменным, и от условия соединения данной связки. Условие соединения ассоциированной связки может быть сформулировано, например, следующим образом: если двум переменным 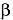, участвующим в связке паттерновой сети, присвоены одинаковые данные, то на этой связке отношение связей 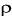-соединено имеет значение ИСТИНА и связка является истинной, а если переменным 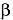связки присвоены разные данные, то отношение связей 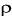-соединено имеет значение ЛОЖЬ и связка является ложной.

Помимо условия соединения связки, определяемого равенством данных, присвоенных в качестве значений двум переменным одной связки, могут быть определены многие иные условия соединения связок паттерновой сети.

Если все связки ассоциированной паттерновой сети являются истинными, то такая сеть называется истинной. Истинная паттерновая сеть, на всех связках которой выполняется одно и тоже условие соединения, называется регулярной.

К регулярным паттерновым сетям можно применять операции преобразования подобия. В общем случае преобразование подобия паттерновых сетей обозначается символом "s", т.е. также как преобразование подобия образующих. В результате применения к регулярной паттерновой сети преобразования подобия s структура сети и ее абстрактный состав остаются неизменными. Но при этом данные об одной модульной системе, присвоенные переменным и вектора компонент и связок сети заменяются новыми данными, определяющими другую модульную систему с тем же скелетом.

Соотношения (4),(5),(6) являются параметрической моделью множества паттерновых сетей, состоящих из n абстрактных или конкретных ориентированных образующих с различными числовыми значениями параметров li,mi,ri. Соотношения (4),(5),(6') являются параметрической моделью множества ассоциированных паттерновых сетей, состоящих из n ассоциированных ориентированных образующих с различными числовыми значениями параметров li,mi,ri.

Из параметрической модели (4),(5),(6') при условии mi=1 получается частная паттерновая модель, с помощью которой можно представить компьютерные гипертексты и наш веб-курс.