Теория графов

Теория графов и графовые сети (или просто графы) используются практически во всех областях знаний, в том числе, в компьютерной науке и практике. В частности, большую часть UML диаграмм можно представить графами. Основное достоинство графов в том, что их можно рисовать на бумаге или экранах компьютеров в виде точек соединенных стрелками и/или линиями. Вместе с тем, связанный граф представляется формально с помощью наборов бинарных отношений и/или множеств, каждое их которых состоит из двух элементов. Графы рисуют на бумаге не только те кто понимают теорию графов, но и люди, которые никогда о ней не слышали. К примеру, любой администратор, изображающий структуру, подчиненных ему подразделений в виде прямоугольников и стрелок между ними, по сути дела, рисует связанный ориентированный граф, хотя он и не знает об этом.

Началом теории графов считается 1736 год, когда вышла в свет статья Эйлера с его знаменитыми рассуждениями о Кенигсбергских мостах. Затем около 100 лет эта статья оставалась единственной, а методы теории графов невостребованными практикой. Интерес к графам появился только в середине 19 века благодаря исследованиям электрических сетей, моделей кристаллов и структур молекул. С тех пор сфера применений теории графов непрерывно расширялась и сегодня она представляет собой мощную формальную систему, имеющую необозримое множество областей практического применения. Естественно, в одной лекции невозможно детально рассмотреть все аспекты теории графов. Поэтому мы поступим иначе и постараемся понять ее сущность повторив ход рассуждений Эйлера о Кенигсбергских мостах.

Итак в Кенигсберге (ныне г. Калининград) течет река Неман. Она омывает два острова. Между берегами реки и островами во времена проживания в Кенигсберге Эйлера существовали 7 мостов, расположение которых показывает план на Рис. 6.1.

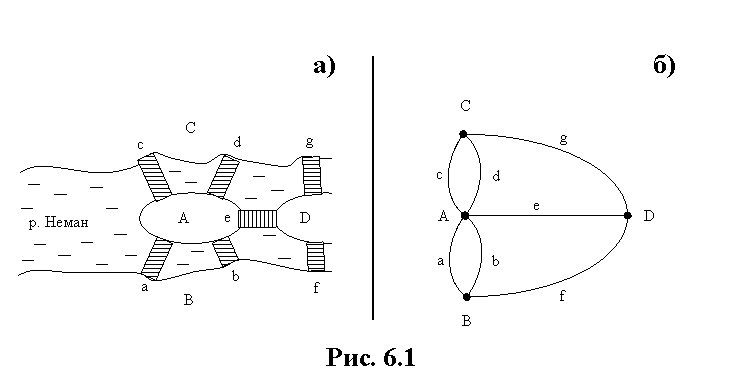
Задача Эйлера состояла в том, чтобы определить, можно ли выйдя из пункта С (или любого другого пункта) пройти каждый мост только по одному разу и вернуться в исходный пункт. Рассуждения и действия Эйлера в ходе решения этой задачи можно представить последовательностью следующих шагов: 1) он нарисовал план, 2) нарисовал неориентированный граф, ассоциированный с берегами, островами и мостами, 3) абстрагировал ассоциированный с данными граф от его содержания (см. Рис.6.1.б); это решающий шаг рассуждений Эйлера, поскольку абстрактный граф можно ассоциировать с чем угодно, например с площадями и улицами между ними, 4) сформулировал и доказал следующую теорему - Конечный граф G является эйлеровым графом тогда и только тогда, когда

а) Граф G связан

б) Все его локальные степени четные.

Поясним, что число ребер, инцидентных одной вершине графа, называется локальной степенью в этой вершине. Мы не будем доказывать эту теорему, которая является второй частью рассуждений Эйлера.

Любой граф может быть нарисован на бумаге или экране компьютера и представлен формально. Поэтому нарисованный на экране компьютера граф может быть транслирован в память компьютера. Покажем каким образом графы рисуются на бумаге и представляются формально на примере трех простейших графов, каждый из которых состоит из одного ребра. Они показаны на Рис. 6.2.

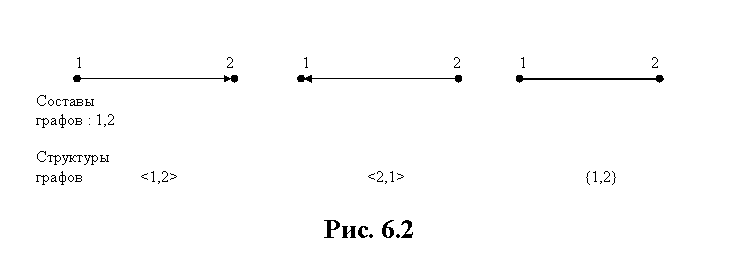
Рис.6.2 раскрывает сущность теории графов в наглядной и формальной формах.

Три задачи для домашнего решения:

1. Построить полный ориентированный граф, моделирующий все родственные отношения в семье, состоящей из отца-Ивана, матери-Марии, сына-Николая и деда Федора (отца отца-Ивана).

2. Построить ориентированный граф, моделирующий все возможные пути однократных обходов двух мостов через реку.

3. Построить полный неориентированный граф, моделирующий листание страниц книги, состоящей из четырех страниц. Определить полное число листаний такой книги.

4. Показать, что оба ассоциированные графа, построенные в задачах 1,3, имеют одинаковую структуру (один и тот же "скелет").