Транспортная задача

Практическая цель управления в транспортной сфере экономики состоит в доставке материальных, финансовых и информационных составляющих потоков в определенные сроки в заданных объемах при минимальных затратах трудовых и материальных ресурсов. Задаче оптимизации транспортных потоков в экономических системах придается первостепенное значение, так как от функционирования транспортной подсистемы глобальным образом зависит эффективность всей экономической деятельности. Предельно совершенным образом организуемая транспортная система впервые была разработана и применена в Японии на заводах фирмы Toyota. Такая система носит название «Канбан» (в переводе с японского - карточка). Суть ее состоит в следующем. Относительно высокая стоимость площадей побудила японские фирмы сводить материально-технические запасы к минимуму. Концепция производства по принципу «точно вовремя» предполагает поступление сырья и комплектующих точно к тому моменту, когда они нужны.

Логико-аналитический метод анализа оценки эффективности систем управления базируется на сетевом моделировании факторов, объектов и показателей с целью их систематизации и взаимоувязки в процессе регулирования материальных, финансовых и информационных потоков.

Транспортная модель используется для составления наиболее экономичного плана пересылки объектов одного вида из нескольких пунктов (например, продукции нескольких заводов) в пункты доставки (например, склады). Такую модель можно использовать в системах управления запасами; в ситуациях, связанных с оборотом наличного капитала; при регулировании информационных потоков и при решении ряда других практических задач.

При построении транспортной модели используются:

1) величины, характеризующие объем производства в каждом исходном пункте и спрос в каждом пункте назначения;

2) стоимость транспортировки единицы продукции из каждого исходного пункта в каждый пункт назначения.

Необходимо понимать, что потребности пункта назначения могут удовлетворяться за счет нескольких исходных пунктов.

Целью построения модели является определение количества продукции, которое следует перевезти из каждого исходного пункта в каждый пункт назначения, с тем чтобы общие транспортные расходы были минимальными. Постулируется, что величина транспортных расходов прямо пропорциональна объему перевозимой продукции.

На рис. 7.2.1 изображена транспортная модель в виде сети с т исходными пунктами и п пунктами назначения. Исходным пунктам и пунктам назначения соответствуют вершины. Дуга, соединяющая исходный пункт с пунктом назначения представляет собой маршрут, по которому перевозится продукция.

Рис. .7.2.1. Сетевая транспортная модель

Обозначим количество продукции, производимой в пункте i, через a_i, а количество продукции, потребляемой в пункте j, - через b_j; c_ij - стоимость перевозки единицы продукции из i в j. Таким образом, транспортная задача сводится к минимизации транспортных расходов z при перевозке из исходного пункта в конечный количества продукции равного x_ij:

минимизировать z =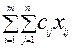

при ограничениях

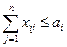, i = 1,2,…,m

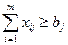, j = 1,2,…,n (*)

x_ij ≥ 0 для всех i и j.

Первая группа ограничений указывает, что суммарный объем перевозок из некоторого пункта не может превышать количества произведенной там продукции; вторая группа ограничений свидетельствует о полной удовлетворенности спроса на продукцию в пункте назначения за счет суммарного объема перевозок.

Если суммарный объем производства некоторой продукции равен суммарному спросу на нее, то такая модель называется сбалансированной транспортной моделью. Тогда:

=

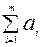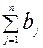
и все ограничения (*) превращаются в равенства:

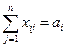, i = 1,2,…,m

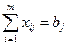, j = 1,2,…,n

В реальных условиях не всегда объем производства равен спросу или превосходит его, однако транспортную модель всегда можно сбалансировать. Проиллюстрируем практически важную идею балансировки на следующих примерах. Рассмотрим вначале стандартную транспортную модель.