Матрица сочетаний возможных состояний среды и ответов испытуемого для ситуации измерения абсолютной чувствительности
| Ответ Стимул | Y – «ДА» | N – «нет» |
| S (стимул есть) | Y/S (правильное обнаружение) | N/S (пропуск стимула) |
| n (стимула нет) | Y/n (ложная тревога) | N/n (правильное отрицание) |
Таким образом, в соответствии с этой матрицей, всего имеется четыре варианта сочетаний:
1) «правильное обнаружение»- стимул в пробе есть и испытуемый дает ответ “Да” (обозначаем как Y/S);
2) «пропуск стимула» - стимул в пробе есть, а испытуемый дает ответ “Нет” (обозначаем как N/S);
3) «ложная тревога» - стимула в пробе нет, а испытуемый дает ответ “Да” (обозначаем как Y/n);
4) «правильное отрицание» - стимула в пробе нет и испытуемый дает ответ “Нет” (обозначаем как N/S).
Из этих вариантов два являются вариантами правильных ответов – правильное обнаружение и правильное отрицание (Y/S и N/n), которые называютсяпринятием правильной гипотезы, а два – ошибочными – пропуск стимула и ложная тревога (N/S и Y/n), которые называем отклонением правильной гипотезы. Ошибочные ответы обозначаются: ошибка первого рода - n/S(пропуск стимула) и ошибка второго рода - Y/n (ложная тревога).
Совершенно очевидно, что значимость для субъекта, принимающего решение, каждого из этих четырех ответов различна и будет определяться целью деятельности, возможными последствиями решений, обстоятельствами и т.д. Для того, чтобы учесть влияние множества таких факторов на процесс принятия решений, вводятся понятия «стоимость решения» ( значимость, важность,…) и «риск» при принятии решения.
Каждый из перечисленных выше четырех вариантов решения имеет свою стоимость (см. табл.5). Знак стоимости (положительный или отрицательный) определяется тем, что это – выигрыш (C11; C22) или проигрыш (C2 1; C12).
Таблица 5
Матрица стоимостей различных вариантов решений в двухальтернативной ситуации
| Ответ Стимул | Y – «ДА» | N – «нет» |
| S (стимул есть) | +C11 (выигрыш) | – C12 (проигрыш) |
| n (стимула нет) | – C2 1 (проигрыш) | +C22 (выигрыш) |
Понятие «риск» отражает величину возможных потерь, которые понесет субъект в результате принятия решения, и является в определенном смысле противоположным стоимости решения.
Условный риск при принятии решения в задаче измерения абсолютной чувствительности будет соответственно равен:
1) При условии наличия сигнала (S):
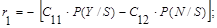 (10a)
(10a)
2) При условии отсутствия сигнала (n):
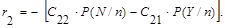 (10b)
(10b)
Наличие знака «–» в этих выражениях отражает уже отмечавшийся выше факт обратных отношений между стоимостью решения (выигрышем) и его риском: чем выше риск, тем меньшим должен быть выигрыш.
Так, если примем равными стоимости выигрышей и проигрышей, то есть C11 = C12 и C2 1 = C22, а также равными все апостериорные вероятности: P(Y/S)= P(Y/N)= P(n /S)= P(n /N)=0,5, то величина условного риска станет нулевой: r1 =r2 = 0. При возрастании стоимости (значимости) правильных ответов (C11; C22) и их апостериорных вероятностей P(Y/S) и P(n /N) абсолютная величина риска снижается. Если же высоки цена неправильных решений и их апостериорные вероятности, то величина риска возрастает.
Общий средний риск (R) тогда будет равен:
R = q1·r1 + q2·r2;(11)
где q1 = P(S) - априорная вероятность появления стимула в пробе;
q2 = P(n) - априорная вероятность отсутствия стимула в пробе.
Самой оптимальной стратегией принятия решений в этих условиях будет та, которая направлена на минимизацию общего среднего риска и, соответственно, получение максимального выигрыша – так называемая «байесовская» стратегия.
Правило принятия решения, соответствующее этой стратегии, будет состоять в учете стоимостей различных четырех исходов в принятии решения (или соответствующих значений рисков) при определении значений порогов принятия решения λ0:

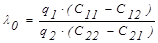 , (12)
, (12)
или, используя новые обозначения,
V1 = C11 – C12,
V2 = C22 – C21,
запишем новое определение для порога принятия решения:
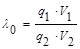 . (13)
. (13)
Соответственно, правило принятия решения будет выглядеть следующим образом:
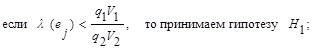 (14а)
(14а)
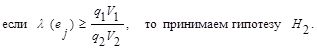 (14b)
(14b)
То есть принимается решение, которое обеспечит максимальный выигрыш (минимальный риск) при имеющихся стоимостях различных исходов, априорных и апостериорных вероятностях. Тем самым обеспечивается учет при принятии решения трех важнейших факторов:
· прогноза возможного состояния среды (априорные вероятности);
· поступившей информации о реально существующем состоянии среды (апостериорные вероятности);
· важности (стоимости) для субъекта различных исходов при принятии решения (величина риска или выигрыша).
Таким образом, при использовании байесовской стратегии принятия решения человек использует всю доступную ему информацию о ситуации для достижения оптимальности решения.
Рассмотрим, как работает такой механизм принятия решения на примере «Охотник» при изменении стоимостей различных исходов, но неизменности априорных и апостериорных вероятностей.
Исходные данные:
Априорные вероятности: q1=0,5; q2=05,. То есть прогноз, который делает охотник, опираясь на информацию, полученную до начала охоты (слухи, мнение товарищей-охотников и местных жителей, и т.п.), таков : «Вероятность встретить на охоте зайца равна 0,5».
Апостериорные вероятности: p(ej /h1)=0,2; p(ej/h2)=0,8. Т.е., отправившись на охоту и проходя по опушке леса, охотник слышит в кустах шорох (ej), весьма похожий на тот, который может вызвать заяц.
Отношение правдоподобия: λ(ej)= 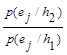 =
= 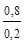 = 4,0.
= 4,0.
Исходя из этих начальных условий, рассмотрим три варианта развития ситуации, различающиеся величиной доходов и расходов охотника (стоимостями исходов).
Вариант1:
Стоимости: цена добытого охотником зайца – 100 рублей;
цена одного патрона – 15 рублей.
C11 = 100 руб.- 15 руб.= 85 руб. (охотник получил прибыль 100 руб. за зайца, но израсходовал 15 руб. на 1 патрон. Таким образом, общий выигрыш охотника составил +85 руб.);
C12= 0 руб. ( охотник зайца не добыл, но и патронов не потратил);
C2 1 = -15 руб. (охотник зайца не добыл, а патрон потратил – таким образом его проигрыш составил -15 руб.);
C22= 0 руб. ( охотник зайца не добыл, но и патронов не потратил).
Порог принятия решения: V1 = C11 – C12 = 85 руб.- 0 руб.= 85 руб.;
V2 = C22 – C21 = 0 руб.- (-15 руб.) = 15 руб.;
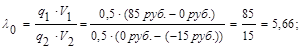
Принятие решения: Применяя сформулированный последним вариант правила принятия решения, получаем:
λ(ej) < λ0 , так как 4,00 < 5,66,
что означает принятие гипотезы H1 – «Заяц есть!» и выполнение соответствующего действия: «Стрелять!».
Вариант 2:
Стоимости: цена добытого охотником зайца – 100 рублей;
цена одного патрона возросла до 30 рублей.
C11 = 100 руб.- 30 руб.= 70 руб. (охотник получил прибыль 100 руб. за зайца, но израсходовал 30 руб. на 1 патрон. Таким образом, общий выигрыш охотника составил +70 руб.);
C12= 0 руб. ( охотник зайца не добыл, но и патронов не потратил);
C2 1 = -30 руб. (охотник зайца не добыл, а патрон потратил – таким образом его проигрыш составил -30 руб.);
C22= 0 руб. ( охотник зайца не добыл, но и патронов не потратил).
Порог принятия решения:
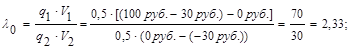
Принятие решения: имеем λ(ej) >λ0 (т.к. 4,00>2,33), следовательно, принимается гипотеза H2 - «Зайца нет!» - и охотник воздерживается от выстрела.
Вариант 3:
Стоимости: возросла цена добытого зайца – 180 рублей;
цена одного патрона - 30 рублей.
C11 = 180 руб.- 30 руб.= 150 руб. (охотник получил прибыль 180 руб. за зайца, но израсходовал 30 руб. на 1 патрон. Таким образом, общий выигрыш охотника составил +150 руб.);
C12= 0 руб. ( охотник зайца не добыл, но и патронов не потратил);
C2 1 = -30 руб. (охотник зайца не добыл, а патрон потратил – таким образом его проигрыш составил -30 руб.);
C22= 0 руб. ( охотник зайца не добыл, но и патронов не потратил).
Порог принятия решения:
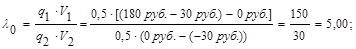
Принятие решения: Имеем λ(ej) < λ0 , так как 4,00 < 5,00, что означает принятие гипотезы H1 – «Заяц есть!» и выполнение соответствующего действия: «Стрелять!».
Таким образом, изменения от варианта к варианту величины расходов и доходов охотника может приводить к разным решениям и, соответственно, разным поступкам.
Интересным является одно из свойств байесова правила принятия решения, появляющееся благодаря связи этого правила с теорией информации – оно требует выбирать ту гипотезу, неопределенность которой на величину logλ0 меньше неопределенности другой гипотезы. Другими словами, человек стремится построить концептуальную модель своих действий с наименьшей потерей информации, добиваясь этим максимальной адекватности своего поведения.
Байесова стратегия принятия решения является оптимальной с точки зрения снижения общего среднего риска при принятии решения. Однако существуют и иные критерии оптимальности для оценки качества принимаемых решений, имеющие не столь общий и универсальный характер. Эти «частные» критерии оптимальности решения и соответствующие им стратегии различаются в зависимости от того, каковы условия, в которых приходится принимать решение, и целями, которые преследуются человеком, принимающим решение.
Так, если не имеется возможности оценить априорные вероятности q1 и q2, использовать байесово правило принятия решения в полной мере невозможно. Однако можно выбрать другие значения этих вероятностей 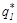 и
и 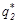 , отличные от реальных q1 и q2 - такие, при которых величина среднего риска R (см. (11)) была бы максимальной при использовании байесовой стратегии. При выбранных таким образом значениях априорных вероятностей, как бы они не отличались от реальных значений q1 и q2, суммарный средний риск R (суммарные потери) будет минимален. Иначе говоря, при этих значениях
, отличные от реальных q1 и q2 - такие, при которых величина среднего риска R (см. (11)) была бы максимальной при использовании байесовой стратегии. При выбранных таким образом значениях априорных вероятностей, как бы они не отличались от реальных значений q1 и q2, суммарный средний риск R (суммарные потери) будет минимален. Иначе говоря, при этих значениях 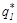 и
и 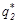 средний риск (потери) будут одними и теми же для любых значений q1 и q2. Действуя таким образом, испытуемый стремится тем самым минимизировать ошибки обоего рода. Стратегия (и критерий), соответственно которой испытуемый выбирает такой вариант действий, называется минимаксной стратегией.
средний риск (потери) будут одними и теми же для любых значений q1 и q2. Действуя таким образом, испытуемый стремится тем самым минимизировать ошибки обоего рода. Стратегия (и критерий), соответственно которой испытуемый выбирает такой вариант действий, называется минимаксной стратегией.
Минимаксный критерий относится к классу байесовых, поскольку в нем также используется отношение правдоподобия. Но по сравнению с байесовым правилом он является более осторожным, и, следовательно, менее оптимальным. Несмотря на явное превосходство байесова критерия над минимаксным при полноте исходных данных, последний при определенных условиях, когда байесов критерий приводит к грубым ошибкам, является «лучшим среди худших». Он предохраняет от слишком больших потерь, которые понес бы тот, кто пользовался бы любым другим правилом принятия решения.
В некоторых задачах, связанных с принятием решения, испытуемый может столкнуться с ситуацией, когда неизвестны ни априорные вероятности, ни стоимости, соответствующие различным типам ответов. В этом случае оптимальной может быть стратегия (критерий) Неймана-Пирсона – фиксируется вероятность ошибок одного рода (в нашем случае – это пропуск стимула или ложная тревога) и используется такое правило принятия решения, чтобы одновременно минимизировать вероятность ошибок другого рода.
Существуют и другие варианты критериев оптимальности – STD (цель – максимизация выигрыша), Зигерта (цель – максимизация процента правильных ответов), критерий 1 рода (цель – минимизировать неопределенность входной информации) и 2 рода (цель – достижение максимально устойчивой деятельности), и т.д., однако их рассмотрение выходит за рамки настоящего пособия.
Дата добавления: 2015-03-09; просмотров: 857;
