Метод постоянных стимулов
Процедура. Вокруг предлагаемого значения порога в диапазоне от очень редко до почти всегда воспринимаемых величин стимула располагается от 5 до 10 равноотстоящих друг от друга на оси I значений стимула (оптимально – 7 градаций). Каждое из этих значений стимула предъявляется в эксперименте равное число раз (т.е. все значения стимула имеют одинаковую частоту предъявления). Количество предъявлений определяется конкретными задачами исследования и может варьировать от 10 до 500. При этом последовательность предъявления этих значений обязательно должна быть случайной – т.е. испытуемый не должен знать, какое из значений стимула будет ему предъявлено в следующей пробе. Его задачей является обнаружение наличия (или отсутствия) стимула в каждой пробе (интервале наблюдения). Т.е. испытуемый должен выбрать один из вариантов ответов- был раздражитель в пробе – «Да», или его там не было - «Нет».
Протокол.Примерная форма протокола приведена в табл.3 для варианта, когда используется 7 значений величины стимула, каждое из которых предъявляется по 10 раз.
Показатели. На основе полученных данных подсчитывается число случаев правильного обнаружения стимулов для каждого из использовавшихся в эксперименте стимульных значений (I), а затем – частоту (вероятность) их правильного обнаружения:
Pобн= m/n. (3)
По полученным результатам строится график зависимости Pобн от I (рис.3) и определяется значение порога Iпор. Графический способ определения порога является самым простым и достаточно точным.
Таблица 3
Образец протокола эксперимента в методе констант
| Ответы испытуемого* | |||||||
| Вел-на стимула I, Поряд- (усл.ед). ковый номер стимула, n | |||||||
| - - - + - - - - - - | - - - - - - - - + - | - + - - + - - - - - | + - + - - - + - - + | + + - + - - + + - + | - + + + - + + + + + | + + - + + + + + + + | |
| Число обнаруженных стимулов, m | |||||||
| Частота обнаружения стимулов, m/n | 0,1 | 0,1 | 0,2 | 0,4 | 0,6 | 0,8 | 0,9 |
*- «+» – ответ «Да»; «-» - ответ «Нет».
За величину порога принимается значение стимула, которое обнаруживается с вероятностью 0,5. Можно использовать как обычную систему координат, так и нормальную систему (z-координаты), что и изображено на рис.4. При использовании z-координат и аппроксимации данных линейной функцией методом наименьших квадратов результат будет наиболее точным. Для нашего примера Iпор= 5,33 усл.ед.
Область применения. Метод постоянных раздражителей позволяет получить наиболее точные значение порога по сравнению с другими методами. Его результаты не искажаются ожиданиями испытуемых относительно очередных значений предъявляемых стимулов, так как порядок их предъявления случаен. Вместе с тем он требует несколько больших затрат времени на проведение исследования и может использоваться там, где главным является точность и надежность измерения, а не быстрота.
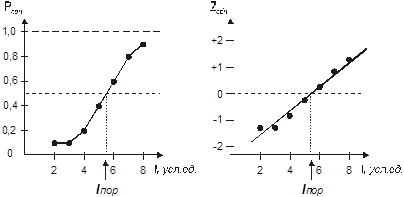 |
Рис.4. Зависимость вероятности правильного обнаружения стимула
(Pобн и Zобн) от его величины (I) (психометрическая функция)
Следует также заметить, что метод постоянных раздражителей в чем-то ближе к современным методам и благодаря в некотором смысле оптимальности сочетания точность/надежность пользуется популярностью у исследователей.
Дата добавления: 2015-03-09; просмотров: 786;
