III. Защита и охрана окружающей среды
Исследование процессов дискретизации и восстановления непрерывных сигналов.
Краткие теоретические сведения
Представление непрерывной функции дискретной последовательностью отсчётов её мгновенных значений. Для точного представления произвольной непрерывной функции x(t) на конечном интервале времени Т необходимо располагать данными о мгновенных значениях (отсчётах) этой функции во всех точках интервала, т. е.
 | |||
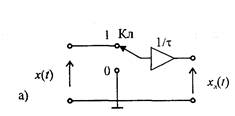 | |||
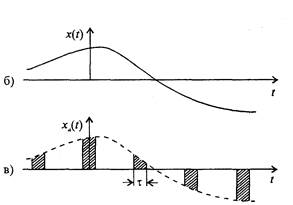
Рис. 6.1. Дискретизация непрерывной функции времени посредством периодической коммутации с частотой дискретизации Fд=1/D
непрерывным множеством отсчётов, отстоящих друг от друга на бесконечно малые интервалы. Некоторое приближённое представление о функции x(t) можно составить по её отображению в виде дискретной последовательности импульсов, имеющих на интервалах D значения x(iD), называемых отсчётами.
Операция замены непрерывной функции последовательностью отсчётов её мгновенных значений называется дискретизацией. В качестве простейшей физической модели дискретизации рассмотрим коммутационное устройство (рис. 6.1, а). С помощью ключа Кл обеспечивается периодическое с частотой дискретизации fд = 1/D подключение к источнику непрерывного сигнала x(t)(рис. 6.1, б) на время t, т.е. производится замена непрерывной функции x(t)последовательностью xд(t) на интервалах t (рис. 6.1, в). Последовательность отсчётов xд(t)можно трактовать как произведение x(t) на периодическую последовательность импульсов дискретизации fд(t) (рис. 6.2):
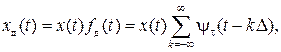
где импульсы дискретизации
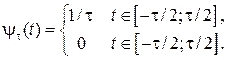
Множитель 1/t нормирует функцию yt(t) к единичной площади. Для этого в схеме рис. 6.1, а после ключа Кл введено масштабное звено. Чтобы перейти к отсчётам мгновенных значений x(t) в точках t = kD, необходимо рассмотреть особенности периодической функции fд(t) при t®0.
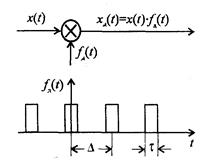 |
Рис. 6.2. Дискретизация непрерывной функции х(t) путем её умножения на периодическую последовательность импульсов fд(t)
Нетрудно видеть, что при t®0 эта периодическая функция заменяется решётчатой функцией 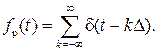
Дискретный сигнал 
|
Спектр периодической последовательности импульсов дискретизации является линейчатым (рис. 6.3, б). Частота дискретизации определяется интервалом дискретизации Fд = 1/D. Спектры дискретизированного сигнала представлены для случаев, когда Fд = 2Fв (рис. 6.3, в), Fд>2Fв (рис. 6.3, г) и Fд < 2Fв (рис. 6.3). Для неискажённого воспроизведения функции x(t) по последовательности отсчётов посредством идеального фильтра низких частот необходимо выбирать частоту дискретизации так, чтобы спектральные компоненты свёртки Sx(t) с каждой из дискретных составляющих периодической функции Fд (p=0, ±1, ±2, ...) располагались в неперекрывающихся областях (рис. 6.3). Этому соответствуют значения Fд³2Fв. При Fд < 2Fв спектральные области перекрываются, в полосу частот (-Fв, Fв) дискретизируемого сигнала попадут спектральные компоненты смежных областей и возникнут искажения при восстановлении функции по отсчётам. Далее будет показано, что для точного воспроизведения непрерывной функции с ограниченным (финитным) спектром достаточно располагать значениями функции (отсчётами) лишь в отдельных точках. Модели сигналов с ограниченным спектром часто используются в технике связи. В частности, в стандартном телефонном канале за верхнюю граничную частоту принимают Fв=3400 Гц, при телевизионной передаче граничная частота определяется числом различимых элементов изображения и равна Fв = 6,5 МГц.
 |
Рис. 6.3
Теорема отсчётов. Фундаментальное значение для решения многих задач теории передачи сигналов имеет следующая теорема отсчётов Котельникова: непрерывная функция х(t), не содержащая частот выше граничной Fв, полностью определяется отсчётами мгновенных значений х(kD) в точках, отстоящих друг от друга на интервалы D£ 1/2 Fв. Интервал D называется интервалом Котельникова. Эта теорема позволяет представить непрерывную функцию x(t) в виде ряда
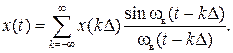 (6.1)
(6.1)
Из сопоставления ряда (6.1) с общим видом обобщённого ряда Фурье в пространстве Гильберта следует, что элементарными базисными функциями в разложении Котельникова являются отсчётные функции:
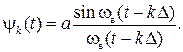 (6.2)
(6.2)
Для коэффициентов разложения x(t) по элементарным функциям (6.2) можем записать
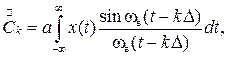 (6.3)
(6.3)
где постоянная а вводится с учётом нормировки функций (6.2). Докажем, что коэффициенты 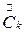 соответствуют мгновенным значениям функции x(t) в точках t =kD . Пусть
соответствуют мгновенным значениям функции x(t) в точках t =kD . Пусть  — преобразование Фурье функции x(t), тогда
— преобразование Фурье функции x(t), тогда
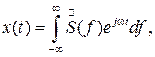
где 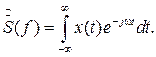 (6.5)
(6.5)
Если x(t) имеет ограниченный спектр с наивысшей частотой Fв, то  вне полосы ±Fв равно нулю, а выражение (6.4) принимает вид
вне полосы ±Fв равно нулю, а выражение (6.4) принимает вид 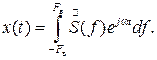 Пусть t= kD, тогда
Пусть t= kD, тогда 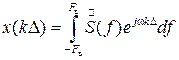 или после подстановки в последнее выражение вместо
или после подстановки в последнее выражение вместо  его значения из (6.5) и изменения порядка интегрирования получим
его значения из (6.5) и изменения порядка интегрирования получим
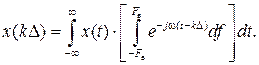
После вычисления интеграла в квадратных скобках
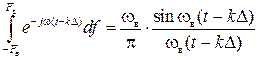
получаем
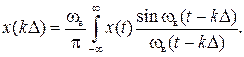 (6.6)
(6.6)
Сравнение (6.6) с (6.3) при 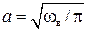 показывает, что коэффициентами обобщённого ряда Фурье
показывает, что коэффициентами обобщённого ряда Фурье 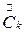 разложения по ортогональным функциям (6.2) являются отсчёты x(kT)/a мгновенных значений функции x(t)/a в моменты t=kD.
разложения по ортогональным функциям (6.2) являются отсчёты x(kT)/a мгновенных значений функции x(t)/a в моменты t=kD.
Восстановление непрерывной функции по отсчётам. Процедура восстановления непрерывной функции x(t) по отсчётам её мгновенных значений х(kD) вытекает непосредственно из (6.1): нужно перемножить значения отсчётов x(kD)на соответствующие отсчётные функции (6.2) и просуммировать полученные произведения. Эти операции иллюстрирует рис. 6.4. Спектральная трактовка процесса восстановления x(t) следует из рис. 6.3.
Для полного восстановления необходимо просуммировать бесконечное множество членов ряда (1). Однако если функция с ограниченным спектром x(t) рассматривается на конечном интервале Т (рис. 6.4, а), то точное разложение (6.1) можно заменить следующим приближённым разложением:
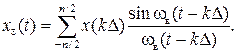 (6.7)
(6.7)
Конечное число отсчётов п, определяющее xe(t), равно (при D = l/2Fв)
n= T/D+1 = 2FвT + 1.
Параметр В = 2FвТ, играющий важную роль в ТЭС, называют базой сигнала. Очевидно, что погрешность представления сигнала при ограничении числа его отсчётов будет тем больше, чем меньшее число слагаемых учитывается при суммировании.
Оценим качественно погрешность 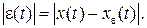 Поскольку все слагаемые ряда (6.1) обращаются при t=iD в нуль во всех точках, за исключением слагаемого с номером k = i, то в этих сечениях значения xe(t) совпадают с x(t), т.е. погрешность e(kD) равна нулю; погрешность достигнет наибольшей величины внутри промежутка между отсчётами. Кроме того, величина погрешности нарастает к краям рассматриваемого интервала.
Поскольку все слагаемые ряда (6.1) обращаются при t=iD в нуль во всех точках, за исключением слагаемого с номером k = i, то в этих сечениях значения xe(t) совпадают с x(t), т.е. погрешность e(kD) равна нулю; погрешность достигнет наибольшей величины внутри промежутка между отсчётами. Кроме того, величина погрешности нарастает к краям рассматриваемого интервала.
Другая причина погрешностей обусловлена тем, что спектры реальных финитных сигналов не обращаются в нуль за пределами граничной частоты. Хотя основная энергия сигналов расположена на частотах от нуля до Fв, некоторая часть приходится на частоты выше граничной. Относительная среднеквадратическая погрешность определяется соотношением
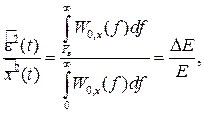 (6.8)
(6.8)
где Е — полная энергия сигнала x(t), а DЕ — та часть энергии, которая оказывается за пределами полосы частот [0, Fв] и не учитывается при восстановлении сигнала. Таким образом, при заданной погрешности (6.8) можно определить необходимую граничную частоту Fв, a следовательно, и интервалы между отсчётами D = 1/2Fв. Детальное исследование показывает, что погрешности за счёт неучитываемой части спектра сигнала будут тем больше, чем медленнее убывает спектр за пределами граничной частоты.
Третьей причиной погрешностей являются неидеальные характеристики фильтра, формирующего отсчётные функции. Колебания, имеющие форму отсчётной функции вида (6.2), можно получить на выходе идеального фильтра нижних частот (ФНЧ) с граничной частотой Fв при действии на его входе дельта-импульса d(t). АЧХ идеального ФНЧ равномерна (рис. 6.5)
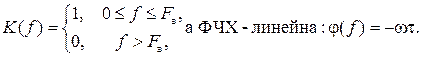
Импульсная характеристика g(t) фильтра определяется обратным преобразованием Фурье от комплексного коэффициента передачи 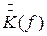 :
:
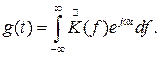
Для рассматриваемого случая идеального ФНЧ
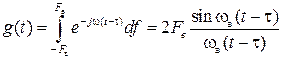 (6.9)
(6.9)
Характеристики реальных фильтров K(f) и j(f) отличаются от идеальных (пунктирные кривые 2 на рис. 6.6), что приводит к отклонению реальной функции отсчётов от идеальной (кривая 2 на рис. 6.6) и, как следствие, к появлению дополнительных погрешностей восстановления функции x(t) по отсчётам.
 |
Рис. 6.6. Импульсная характеристика: (1) для идеального ФНЧ, (2) для неидеального ФН
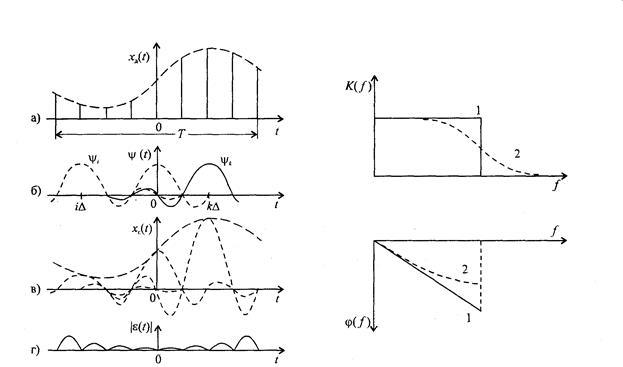
Рис. 6.4. Иллюстрация принципа восста- Рис. 6.5. АЧХ и ФЧХ фильтра,
новления непрерывной функции по ее формирующего отсчетные функ-
отсчетам ции: (1) идеального ФНЧ;
(2) неидеального ФНЧ
Схема работы и измерительная аппаратура
Исследуемое устройство (рис. 6.7) размещено на сменном блоке ТЕОРЕМА КОТЕЛЬНИКОВА и представляет собой дискретизатор (обозначенный на макете как перемножитель сигналов) и набор из трех фильтров - восстановителей с разными частотами среза. Источники исследуемых сигналов - s1, s2 и s3 находятся в блоке ИСТОЧНИКИ СИГНАЛОВ, а сами сигналы представляют собой суммы гармоник с частотами 2, 4 и 6 кГц. (При необходимости исследуемый сигнал может быть усложнен добавлением еще одного гармонического сигнала с частотой 1 кГц с помощью сумматора стенда).
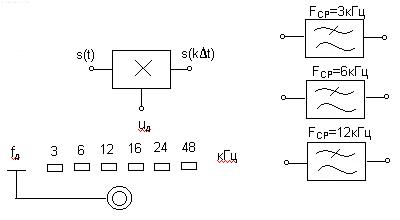
Рис. 6.7.
Дискретизатор, формирующий отсчеты s(kDt) непрерывного сигнала s(t), выполняет функцию перемножителя этого сигнала на короткие импульсы напряжения дискретизации (uдискр). В данном случае дискретизатор выполнен по схеме аналогового коммутатора, пропускающего входной сигнал s(t) на выход в течение короткого времени существования импульсов дискретизации. Временной интервал между соседними отсчетами дискретизированного сигнала s(kDt) зависит от выбора частоты дискретизации fд:
Dt=1/fд.
Эта частота может изменяться дискретно при нажатии кнопки fд, при этом выбранное значение этой частоты индицируется светодиодом (fд=3,6,12,16,24 и 48 кГц). Все упомянутые выше частоты (частоты дискретизации и частоты гармоник исследуемых сигналов) жестко синхронизированы, что упрощает наблюдение процессов на осциллографе.
В качестве фильтров - восстановителей используются три активных ФНЧ третьего порядка с частотами среза 3, 6 и 12 кГц. Для снятия импульсных характеристик фильтров используется генератор коротких импульсов "d - функций" (гнезда d(t) в блоке ИСТОЧНИКИ СИГНАЛОВ).
В соответствии с теоремой Котельникова отсчеты, следующие через интервалы времени Dt=1/2FВ, где FВ - верхняя частота сигнала, могут быть преобразованы в исходный сигнал после прохождения через идеальный ФНЧ с частотой среза FСР = FВ. В работе используются реальные ФНЧ с достаточно крутыми спадами АЧХ после частоты среза. Поэтому на практике выбирают Dt несколько меньше (а иногда и в несколько раз меньше), чем требуется в теореме Котельникова с тем, чтобы реальный ФНЧ с АЧХ трапециевидной формы позволял выделить спектр исходного сигнала из спектра дискретизированного сигнала, что гарантирует отсутствие искажений при обратном преобразовании (восстановлении) сигнала.
В качестве измерительных приборов используются двухлучевой осциллограф и ПК, работающий в режиме анализатора спектра.
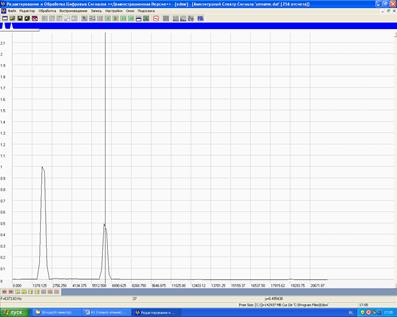 Амплитудный спектр сигнала
Амплитудный спектр сигнала
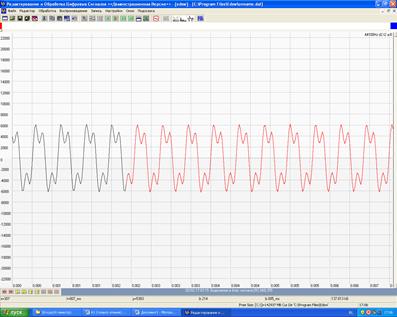 Временная диаграмма S3
Временная диаграмма S3
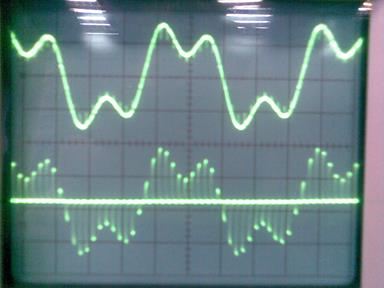 Осциллограммы сигналов
Осциллограммы сигналов
При частоте дискретизации 12 кГц
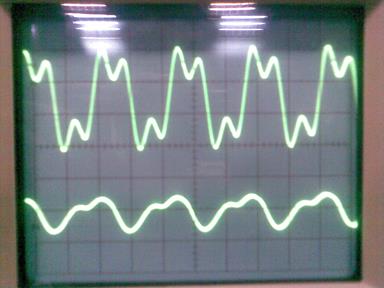 Осциллограмма 1 фильтр
Осциллограмма 1 фильтр
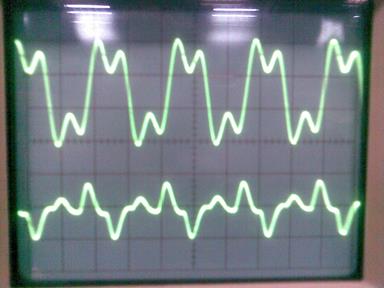 Осциллограмма 2 фильтр
Осциллограмма 2 фильтр
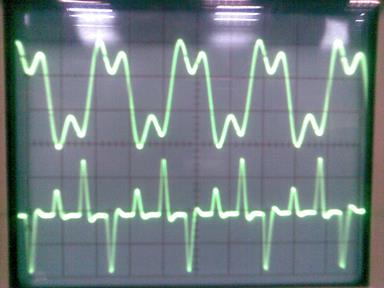 Осциллограмма 3 фильтр
Осциллограмма 3 фильтр
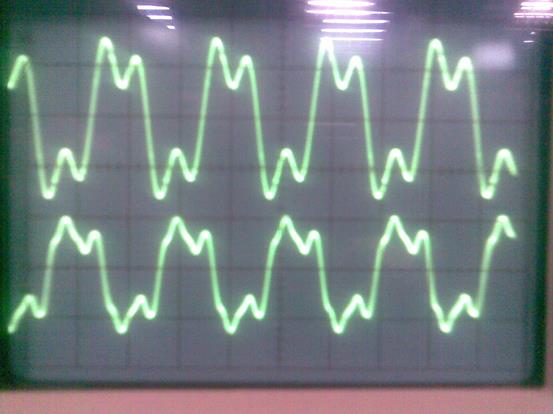
При корректированной частоте 16 кГц с 2 фильтром
III. Защита и охрана окружающей среды
Дата добавления: 2015-01-15; просмотров: 2819;
