Правило принятия решения
Правило принятия решения, которым будет руководствоваться испытуемый в этом случае, будет достаточно простым:
если sj > s0 , то принимается решение «Да, стимул был» (гипотеза h1);
если sj < s0 , то принимается решение «Нет, стимула не было» (гипотеза h2).
Для того, чтобы субъект мог дать один из этих ответов, необходимо определить то критическое значение s0, которое разделит всё множество значений s на две области, соответствующие ответам ²ДА² и ²НЕТ².
Процедура определения s0 задаётся теми закономерностями процесса принятия решения, которые рассмотрели ранее в разделе 2. Однако теперь рассматриваются уже не дискретные величины апостериорных вероятностей p(ej /h1) и p(ej /h2), а функции распределения плотности вероятности возникновения сенсорного события при наличии (или без) стимула в пробе - f(s) и f(n) соответственно (см. рис.6). А взамен отношения правдоподобия λ используется функция отношения правдоподобия f(λ), которая для случая нормального закона распределения функций f(s) и f(n) является монотонно возрастающей:

 , (15)
, (15)
а ее общий вид представлен на рис.7.
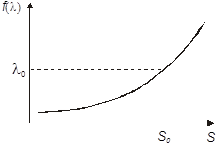 |
Рис.7. Общий вид функции отношения правдоподобия
Порог принятия решения λ0 определяется субъектом в полном соответствии с правилами, описанными ранее в разделе 2 - исходя из имеющихся значений априорных вероятностей qs, qn и стоимостей решений C. Затем, через функцию отношения правдоподобия f(λ) определяется пороговое значение s0 , которое и позволяет принимать решение о переводе сенсорного события в категорию «сенсорный образ Š».
Соответственно четырём типам исходов (см. таблицу 4), можно определить их вероятности, если определены λ0 и s0:
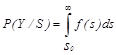 - вероятность правильного обнаружения стимула (16a)
- вероятность правильного обнаружения стимула (16a)
(далее будем обозначать как Pобн);
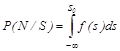 - вероятность пропуска стимула (Pпроп); (16b)
- вероятность пропуска стимула (Pпроп); (16b)
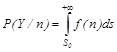 - вероятность ложной тревоги (Pлт); (16с)
- вероятность ложной тревоги (Pлт); (16с)
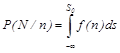 - вероятность правильного отрицания (Pотр). (16d)
- вероятность правильного отрицания (Pотр). (16d)
Графически эти четыре вероятности представляют собой площади под графиками функций f(s) и f(n), изображенными на рис.6., слева и справа от критической точки s0. На рис.6 заштрихованы площади, соответствующие Pобн и Pлт.
При этом:
Pобн+ Pпроп =1, (17а)
Pлт + Pотр =1. (17b)
Учитывая эти соотношения, очевидно, что для полного описания ситуации достаточно знать одну величину из первого равенства (Pобн или Pпроп), и одну - из второго (Pлт или Pотр).
Дата добавления: 2015-03-09; просмотров: 782;
