Рабочая характеристика наблюдателя (РХ)
В качестве основной характеристики сенсорной системы, принимающей решения в соответствии с рассмотренным правилом, принято рассматривать функцию, выражающую зависимость вероятности правильного обнаружения стимула Pобн от вероятности ложной тревоги Pлт. Эта функция получила название «рабочая характеристика наблюдателя» (сокращенно – РХ).
Если принять, что распределение плотностей вероятностей f(s) и f(n) подчиняется нормальному закону распределения, то функция РХ будет обладать следующими особенностями:
· она существует от 0 до 1,является монотонной и выпуклой;
· расстояние между математическими ожиданиями Ms и Mn(см. рис.6), нормированное по s, есть расстояние до кривой РХ от главной диагонали в срединной точке РХ;
· отношение правдоподобия λ есть тангенс угла между горизонталью и касательной, проведенной к РХ в любой ее точке.
На рис.8 изображены варианты кривых РХ в обычной системе координат.
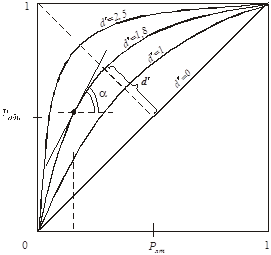
Рис. 8. Рабочая характеристика наблюдателя (РХ)
Допущение о нормальности распределений плотностей вероятностей f(s) и f(n) является в определенном смысле произвольным, так как принимается исходя из общих соображений о том, что процесс формирования сенсорных величин s скорее всего подчиняется именно этому закону, а не какому-либо иному. Если же по каким-то причинам имеется основание полагать, что распределения f(s) и f(n) не являются нормальными, то, соответственно изменится и вид РХ. На рис.9 приведены случаи с треугольным и прямоугольным видами распределений плотностей вероятностей и соответствующие им варианты РХ.
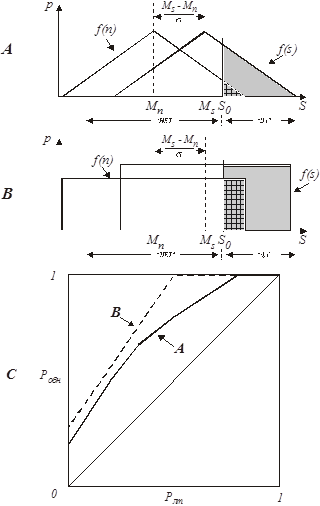
Рис.9. Различные варианты распределений f(s) и f(n) (A и B) и соответствующие им рабочие характеристики (C)
3.2.4. Показатель чувствительности d¢
В качестве основного показателя, характеризующего чувствительность сенсорной системы, принимается величина d¢ :

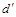 =
= 
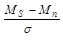 , (18)
, (18)
где s =ss=sn, а ss и sn – стандартные отклонения распределений f(s) и f(n).
Величина d¢ показывает, насколько далеко по оси s отстоят друг от друга распределения f(s) и f(n) – это зависит от значения числителя в правой части формулы (18), а также насколько хорошо они могут быть различимы субъектом – что зависит от значения знаменателя – величины s.
Таким образом, абсолютная чувствительность сенсорной системы определяется, согласно этой формуле:
a) величиной внутреннего сенсорного шума - т.е. значением Mn;
b) величиной сенсорного эффекта, вызванного стимулом – Ms;
c) дисперсией величин а) и b) - ss и sn.
На рис.8 дана графическая интерпретация значения показателя d¢ - это расстояние от главной диагонали до срединной точки кривой РХ.
Диапазон изменений количественных значений величины d¢ находится в следующих пределах:
0 ≤ d¢ ≤ 6,
при этом для значения верхней границы дана некоторая условная величина, вытекающая из данных, которые могут быть получены в реальном эксперименте, а не теоретически возможная.
Очень важным свойством показателя d¢ является то, что d¢ не зависит от значения порога принятия решения λ0, который, в свою очередь, определяется несенсорными факторами (например, мотивацией испытуемого или значимостью для него различных вариантов ответа). Тем самым разделяются собственные свойства сенсорной системы (чувствительность - d¢), и характеристики процессов принятия решения (отражающиеся в значении λ0).
Именно это свойство d¢ обуславливает принципиальное отличие этого показателя от классических мер чувствительности - порогов чувствительности. В чём же это отличие? И в чём преимущество показателя чувствительности d¢ по сравнению с пороговыми мерами?
С этой целью сопоставим показатель d¢ и величину порога, измеренную методом постоянных раздражителей (констант), а также проанализируем, к чему может привести неучет влияния внесенсорных факторов (порога принятия решения l0) при оценке абсолютной чувствительности.
Предположим, что при проведении исследования использовано 5 значений стимула I: I 1; I 2; I 3; I 4; I 5. На сенсорной оси s каждому из этих значений будут соответствовать 5 распределений плотности вероятности сенсорных эффектов f1, f2, f3, f4, f5, с математическими ожиданиями Ms1; Ms2; Ms3; Ms4; Ms5, а также одно распределение f(n) с математическим ожиданием Mn. Графически это отражено на рис.10.

Рис.10. Распределения плотности вероятности сенсорных эффектов, вызываемых воздействием пяти использованных значений стимула в методе констант
В соответствии с процедурой метода констант, описанной в разделе 1.4, по итогам проведенного эксперимента была построена психометрическая функция и рассчитано значение нижнего абсолютного порога чувствительности I (1)пор.
Спустя некоторое время, с этим же испытуемым проводится ещё один точно такой же эксперимент. Однако теперь увеличиваем стоимость (субъективную значимость) ложных тревог (ЛТ). В инструкции, предлагаемой испытуемому перед экспериментом, экспериментатором всячески подчёркивается, что испытуемый не должен ни в коем случае допускать ошибок такого рода. И если у испытуемого возникнет малейшее сомнение в том, что в пробе был предъявлен стимул, то лучше дать ответ «Нет. Стимула не было». Тем самым, согласно изложенному ранее правилу принятия решения и стратегии ПР, мы сдвигаем порог принятия решений λ0 и, соответственно, пороговое значение s0 на оси s.
Что из этого получается, видно из рисунка 11. Испытуемый, стремясь минимизировать число ложных тревог, одновременно вынужден снижать число правильно обнаруживаемых стимулов, т.е. уменьшает вероятность правильного обнаружения Pобн для тех же значений стимула по сравнению с первым экспериментом.
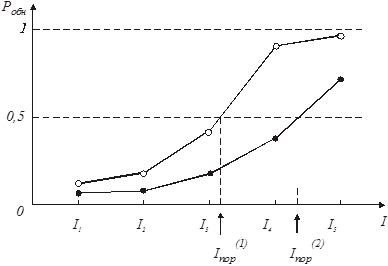
Рис.11. Изменение психометрической функции и значения порога, получаемые в методе констант при изменении порога принятия решения l0.
Следствием этого процесса является новая психометрическая функция и иное значение порога чувствительности - I (2)пор, существенно отличающееся от полученного ранее. Налицо явное противоречие – у одного и того же испытуемого в одних и тех же условиях проведения эксперимента получены разные значения порога и совершенно неясно, какое из них должно считаться «истинным». В некоторых же случаях возможно возникновение совершенно парадоксальной ситуации, когда рассчитываемая величина порога может принимать нулевые или даже отрицательные значения.
Если ещё раз изменим λ0 и проведем новую экспериментальную серию, то получим ещё одно значение Iпор, и т.д. Этой несуразицы можно избежать, если использовать в качестве показателя чувствительности d¢, который не меняется при изменении λ0.
Дата добавления: 2015-03-09; просмотров: 835;
