Оценки коэффициентов функции отклика

Эксперимент, проведенный по плану, представленному в табл. 3.1, позволяет оценить коэффициенты неполного полинома третьей степени y^' = b₀ + b₁x₁ + b₂x₂ + bх₃ + b₁₂x₁x₂ + b₁₃x₁x₃ + b₂₃x₂x₃ + b₁₂₃x₁x₂х₃ или линейной функции y^' = b₀ + b₁x₁ + b₂x₂ + bх₃. Первый вид полинома позволяет оценить не только влияние отдельных факторов, но и один из часто встречающихся видов нелинейности, когда эффект одного фактора зависит от уровня других факторов, т.е. присутствует эффект взаимодействия факторов. Эффект взаимодействия вида x_i x_j называют парным, x_i x_j x_k – тройным и т.д. С ростом количества факторов число возможных взаимодействий быстро увеличивается. Суммарно количество всех коэффициентов функции отклика такого типа равно числу опытов полного факторного эксперимента.

Оценки коэффициентов полинома определяются на основе метода наименьших квадратов и для рассматриваемого типа ПФЭ вычисляются по простым соотношениям [8, стр. 29]

; .

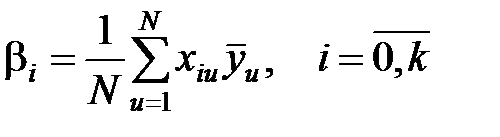(3.1)

Здесь величина соответствует значению отклика в указанной точке факторного пространства при отсутствии повторных опытов или является оценкой математического ожидания 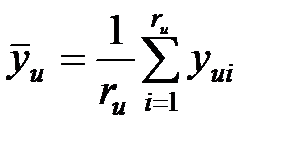значений функции отклика по всем r_u повторным опытам в данной точке. Повторные опыты проводятся в тех случаях, когда на функционирование системы оказывают влияние случайные воздействия. Количество повторных опытов в разных точках плана может различаться.

Допустима следующая интерпретация оценок коэффициентов:

b₀ соответствует значению функции отклика в центре проводимого эксперимента;

b_i равен приращению функции при переходе значения фактора i с нулевого уровня на верхний (это вклад фактора в значение функции);

b_ij равен нелинейной части приращения функции при одновременном переходе факторов i и j с нулевого уровня на верхний и т.п.

Ошибки в определении коэффициентов полинома можно охарактеризовать соответствующей дисперсией. С учетом того, что кодированные значения факторов принимают значения +1 и ­– 1, оценка дисперсии коэффициента определяется соотношением

.

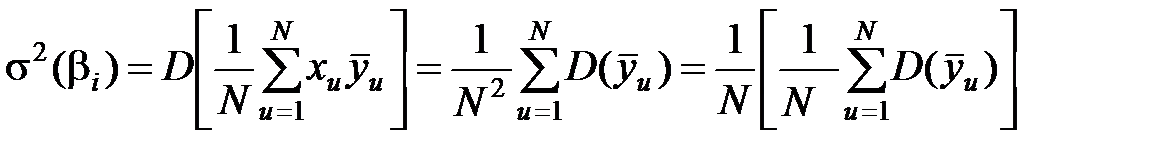(3.2)

Следовательно, оценка дисперсии всех коэффициентов одинакова и определяется только дисперсией средних значений функции отклика и числом опытов. Эту формулу можно применять, если количество опытов во всех точках плана одинаково. При факторном эксперименте, в отличие от классического, одновременно варьируются все факторы, поэтому каждый коэффициент полинома определяется по результатам всех экспериментов, тем самым оценка дисперсии коэффициентов получается в N раз меньше средней дисперсии всех опытов. Оценка дисперсии среднего значения в конкретной точке плана 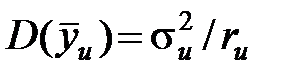, где s_u² – оценка дисперсии функции отклика в точке u, r_u – число повторных опытов в этой точке плана [7, стр. 50]. Дисперсия оценок всех коэффициентов одинакова, поэтому ПФЭ рассмотренного типа являются ротатабельным.

При использовании неполных полиномов k-го порядка количество точек плана равно количеству оцениваемых параметров. Поэтому не остается степеней свободы для проверки гипотезы об адекватности представления результатов эксперимента заданной математической моделью. Если применять полиномы первой степени, то тогда остаются степени свободы для проверки гипотезы об адекватности модели.