Способы градиентной оптимизации

Существует несколько модификаций метода градиентной оптимизации применительно к дискретным вычислениям [4].

Если подъем происходит поочередно по каждой отдельной координате v₁, v₂, … , v_k , то такой метод называют покоординатным подъемом или методом Гаусса – Зейделя. Движение осуществляется из некоторой точки по координате v₁ до тех пор, пока не станет равной нулю соответствующая производная ¶f(V) / ¶v₁ = 0. Все остальные координаты (аргументы функции) сохраняют постоянное значение. После этого подъем начинается по другой координате. Порядок перебора координат не играет принципиальной роли, а влияет только на скорость поиска, поэтому обычно начинают с v₁, затем с v₂ и т.д. После того, как будет произведен подъем по всем координатам, начинают повторно с v₁. Процесс заканчивается, когда все частные производные будут равны нулю (будут меньше порога чувствительности).

Метод наискорейшего подъема предполагает определение градиента в исходной точке, далее подъем в этом направлении осуществляется до тех пор, пока производная df(V) / dV в этом направлении не обратится в нуль. После этого снова определяют градиент и осуществляют по нему подъем до нулевого значения производной и т.д. Модификация этого метода предусматривает вычисление градиента в каждой новой точке траектории перемещения.

Все сказанное о сущности методов поиска максимума функции легко транспонируется и для поиска минимума. Рассмотренные выше методы предполагают возможность движения по любому выбранному направлению, т. е. ограничений на область допустимых значений аргументов нет. В качестве начальной точки может быть взята любая точка пространства E_k. Равенство Ñf(V^*) = 0 является необходимым, но не достаточным условием экстремума функции в точке V^*, да и точек V^* может быть несколько. Поэтому требуются дополнительные исследования для установления, какая из точек действительно является оптимумом (а не точкой перегиба) и какая из них является глобальной.

Одна из основных проблем применения градиентного метода поиска заключается в выборе величины каждого дискретного шага. Шаги могут быть постоянными или переменными. Второй вариант в реализации алгоритма более сложный, но обычно требует меньшего количества итераций.

Поиск максимума функции включает следующие этапы.

1. Определение аналитических соотношений для вычисления градиента функции Ñf(V), длины вектора градиента |Ñf(V)| и единичного вектора t(V), используя соответственно формулы (2.1), (2.2) и (2.3).

2. Выбор исходной точки V_n при n = 0 (начальных значений аргументов функции).

3. Вычисление координат единичного вектора t(V_n) по формуле, полученной на шаге 1 и определение координат новой точки при движении по направлению единичного вектора.

4. Выбор шага a изменения координат текущей точки V_n.Осуществляется из условия предельного увеличения функции f[V_n + at(V_n)] одного аргумента a в соответствии с уравнением

.

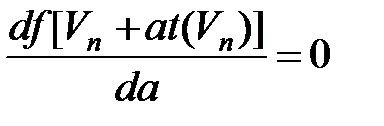(2.4)

Корень этого уравнения, максимизирующий функцию f(V), обозначим a_n. Следующее приближение V_{n + 1} вычисляется по формуле

V_n+1 = V_n+а_n t(V_n).

Производится возврат к этапу 3.

В результате формируется последовательность приближений V₀, V₁, V₂, … . Вычислительный процесс заканчивается, когда будет достигнута точка V_n, в которой оценка градиента будет равна нулю (коэффициенты функции отклика становятся незначимыми).

Пример 2.2.1. Выполнить шаг крутого восхождения для функции отклика у = – 3х₁² – 2х₂².

Решение.

Этап 1. Общий вид градиента функции Ñf(V):

¶у/¶х₁ = – 6х₁, ¶у/¶х₂ = – 4х₂ ; Ñf(V) = (– 6х₁; – 4х₂).

Длина вектора градиента:

|Ñf(V)| = [(¶у/¶х₁)²; (¶у/¶х₂)²]^0,5 = [36 х₁²; 16х₂² ]^0,5 ;

Единичный вектор t:

t = (t₁; t₂) = Ñf(V) / |Ñf(V)| = – (6х₁; 4х₂) / [36 х₁² +16х₂² ]^0,5 .

Этап 2. Выбор начальной точки, например V₀ = (5; 3).

Этап 3. Вычисление координат единичного вектора

t(V₀)= –(30; 12)/[36·25 + 16·9]^0,5= – (30; 12)/[32,31] = (–0,93; –0,37).

Координаты точки V₁ при движении по направлению вектора t

V₁ =V₀ + a·t(V₀)= (5; 3) + a·(– 0,93; – 0,37) = (5 – a·0,93; 3 – a·0,37).

Функция отклика у в точке V₁ пространства двух переменных

у = – 3·(5 – a·0,93)² – 2·(3 – a·0,37)².

Этап 4. Выбор шага а изменения координат текущей точки в соответствии с уравнением (2.4)

32,34 – 5,737·а = 0.

Следовательно, шаг а = 5,637.

Координаты точки V₁ после выполнения первого шага крутого восхождения V₁ = V₀ + а·t(V₀) = (– 0,242; 0,914).

Аналогично выполняется следующий шаг крутого восхождения.

Рассмотренный алгоритм применяют только для нелинейных функций. Если функция отклика является линейной, то выбор оптимального значения параметра a невозможен. В этом случае шаг выбирается исходя из эвристических предположений исследователя о виде функции отклика.

Особенности применения градиентной оптимизации совместно с методами планирования экспериментов

Применение методов планирования экспериментов вносит в типовую процедуру градиентных методов поиска свою специфику.

1. В задачах экспериментального исследования функция f(V) обычно изначально неизвестна, ее вид выбирается относительно произвольно, а параметры устанавливается по результатам эксперимента. На начальных этапах исследования трудоемкость решения задачи оптимизации можно снизить, применяя неполные полиномы k-го порядка или линейные полиномы

Таким образом, вместо самого градиента применяется его оценка. Оба вида полинома являются линейными относительно конкретного фактора. Количество членов полинома типа (2.5а) составляет 2^k , а для типа (2.5б) равно k+1.Теоретически оценки коэффициентов в точке оптимума должны стать равными нулю, что и будет признаком завершения поиска решения. Однако применение этих моделей может стать нерациональным в области, близкой к оптимуму, из-за больших относительных погрешностей в оценке коэффициентов указанных моделей. Поэтому для исследования области оптимума следует переходить к использованию полиномов более высокой степени.

2. Применение градиентных методов предполагает, что движение по градиенту может осуществляться в любом направлении изменения аргументов функции f(V), т.е. ограничений на область допустимых значений аргументов нет. В практических задачах всегда существуют ограничения на значения параметров, поэтому при выборе направления движения следует учитывать это обстоятельство.

3. Значение градиента зависит от принятой системы перехода к кодированным значениям переменных, т.е. не является инвариантным к выбору центральной точки и интервала варьирования в формуле (1.1). Но знаки частных производных при переходе от одной системы координат к другой сохраняются. Поэтому направление перемещения в методе градиентного поиска не меняется при смене системы координат. Следовательно, в любой системе координат градиентный метод приведет к оптимуму, хотя скорость поиска и будет зависеть от выбранных значений центра и интервала варьирования переменных.

4. Рассмотренный выше способ определения шага крутого восхождения применяют только при описании поверхности отклика полными полиномами второй или более высокой степени. При анализе линейных функций определение шага изменения аргументов производится на основе неформальных процедур. Для полиномов (2.5а, б) шаг Dv_i^* изменения i-го фактора относительно центра (в центре области планирования все нормализованные переменные равны нулю) определяется пропорционально соответствующей составляющей оценки градиента и величине интервала варьирования Dv_i

Новое значение основного уровня фактора v_i,1 в исходной шкале измерений составит величину v_{i, 1}= v_{i, 0} + Dv_i^*.

5. Применение метода крутого восхождения в его классическом виде предполагает вычисление градиента на каждом этапе. А это означает необходимость проведения достаточно большого количества опытов. Бокс и Уилсон предложили в 1951 г. модификацию метода крутого восхождения. Они рекомендуют на начальном этапе поиска применять линейные полиномы для описания функции отклика. Значение градиента оценивается в начальной точке, после чего пошаговое движение по градиенту продолжается до попадания в частный оптимум (до тех пор, пока значение функции отклика возрастает при переходе от точки к точке). В точке частного оптимума с помощью факторного эксперимента снова определяется градиент. И пошаговое движение начинается по новому направлению. Так продолжается до попадания в область глобального экстремума. Эта область не может быть адекватно описана линейным уравнением. Поэтому переходят к более точному описанию поверхности отклика на основе полиномов второго порядка и уточнению положения точки глобального оптимума. Построение плана для формирования полинома второй степени производится путем добавления некоторых точек к "ядру", уже сформированному для линейного приближения (такие планы получили наименование композиционных). В целом метод Бокса – Уилсона во многих случаях требует меньшего количества опытов возможно при несколько большем числе шагов.

6. Градиентные методы не обеспечивают гарантированного нахождения глобального оптимума при нарушении условия унимодальности функции отклика. Выбор начальной точки для крутого восхождения предопределяет область поиска локального экстремума. Поэтому при наличии априорных сведений о возможности существования нескольких локальных экстремумов, целесообразно осуществить решение задачи оптимизации для нескольких вариантов задания исходных значений параметров.

7. Если эксперимент проводится на реальном объекте и требует больших затрат ресурсов, то поиск значений параметров может завершиться при получении удовлетворительных, а не оптимальных, значений функции отклика. Градиентный метод позволяет находить приемлемые решения и в этом случае.

Однако градиентный метод не всегда эффективен. Например, если поверхность функции отклика имеет овражный характер, то движение будет происходить с одного склона на другой с медленным продвижением к точке минимума. Для таких функций разработано несколько эвристических методов ускоренного продвижения вдоль оврага или гребня.

ПЛАНЫ ДЛЯ РЕШЕНИЯ ЗАДАЧ ОПТИМИЗАЦИИ