Постановка задачи оптимизации
Поиск оптимальных значений параметров является одной из важных задач, решаемых при создании новых технических систем, управлении производством или технологическими процессами. В соответствии с теорией эффективности необходимо [1]:
сформировать критерий эффективности (функцию отклика в терминах ТПЭ). В большинстве случаев эффективность определяется совокупностью показателей, характеризующих частные свойства исследуемой системы и выполняемой ею операции. Критерий эффективности строится на множестве значений частных показателей с использованием теории полезности или методов векторной оптимизации. В некоторых случаях критерий эффективности удается построить на множестве значений одного показателя, переведя все остальные показатели в разряд ограничений;
выделить управляемые и неуправляемые параметры (факторы) системы и среды, оказывающие существенное влияние на критерий эффективности;
определить ограничения на значения параметров.
Задача оптимизации заключается в нахождение экстремума функции отклика в области допустимых значений параметров. Чтобы найти экстремум, необходимо иметь описание поверхности отклика в диапазоне варьирования параметров, что далеко не всегда удается получить исходя из теоретических соображений, так как функция отклика в аналитическом виде может быть априори неизвестна.
Реализация задачи оптимизации, основанная на применении ТПЭ, как и любой задачи экспериментального исследования, начинается с определения объекта анализа, цели исследования, изучении сущности исследуемого процесса, анализе имеющихся ресурсов, возможности проведения экспериментов с изучаемым объектом в необходимом диапазоне изменения факторов.
Объектом анализа выступает заданный критерий эффективности исследуемой системы, рассматриваемый как функция от существенных параметров системы и внешней среды. Система может представлять собой реальный физический объект или его модель – физическую или математическую (имитационную, сложную аналитическую).
Изучение процесса функционирования объекта позволяет выявить факторы, оказывающие существенное влияние на функцию отклика. Выбор существенных переменных потенциально определяет степень достижения адекватности получаемой модели: отсутствие в исходном перечне существенных параметров, да еще и произвольно меняющихся в ходе эксперимента, не позволяет правильно решить задачу оптимизации; включение несущественных параметров усложняет модель, вызывает значительное увеличение объема экспериментов, хотя по результатам исследования несущественность соответствующих параметров будет выявлена.
Для каждой переменной следует определить диапазон и характер изменения (непрерывность или дискретность). Ограничения на диапазон изменений могут носить принципиальный или технический характер. Принципиальные ограничения факторов не могут быть нарушены при любых обстоятельствах. Эти ограничения задаются исходя из физических представлений (например, емкость устройств памяти всегда имеет положительное значение). Второй тип ограничений связан с технико-экономическими соображениями, например, с наличием соответствующего аппаратно-программного комплекса, принятой технологией обработки информации.
Выделение области изменения факторов является не формальной задачей, а основывается на опыте исследователя. В рамках области допустимых значений факторов необходимо выделить начальную область планирования эксперимента. Этот выбор включает определение основного (нулевого) уровня как исходной точки построения плана и интервалов варьирования. Интервал варьирования задает относительно основного уровня значения фактора, при которых будут производиться эксперименты. Обычно интервалы являются симметричными относительно центрального значения. Интервал варьирования должен отвечать двум ограничениям: его применение не должно приводить к выходу фактора за пределы области допустимых значений; он должен быть больше погрешности задания значений фактора (в противном случае уровни фактора станут не различимыми). В пределах этих ограничений выбор конкретного значения является неформальной процедурой, учитывающей ориентировочную информацию о кривизне поверхности функции отклика.
Фактор должен быть управляемым, т.е. экспериментатор может поддерживать его постоянное значение в течение всего опыта. Для фактора необходимо указать его конкретные значения и средства контроля. Сам фактор должен быть первичным, ибо сложно управлять фактором, который в свою очередь является функцией других факторов. Для каждого фактора следует указать точность его задания и поддержания в ходе эксперимента.
Одновременное изменение факторов предполагает их совместимость, что означает осуществимость и безопасность всех их сочетаний. Необходимо также обеспечить независимость изменения каждого фактора, что означает возможность установления любого значения фактора вне связи со значениями других факторов.
Цель исследования, требуемая точность получаемых результатов, имеющиеся ресурсы ограничивают множество допустимых моделей функции отклика (с усложнением модели и повышением точности оценки показателей резко возрастает объем необходимых опытов) и соответственно предопределяют план проведения экспериментов.
3.2. Полный факторный эксперимент типа 2k
На начальных этапах оптимизации для определения градиента применяют неполные полиномы второго порядка или линейные полиномы [2, 5, 6]. Вычисление оценок коэффициентов таких полиномов осуществляется на основе обработки результатов реализации наиболее простых планов, в которых каждый фактор принимает только два значения vi min или vi max, расположенные симметрично относительно нулевого уровня или центра плана по данному фактору. Значения уровней варьирования выбирает исследователь, исходя из возможного диапазона изменения каждого фактора и возможности применения линейной аппроксимации функции отклика в выбранном диапазоне изменений параметра. Без ограничения общности можно считать, что кодированные значения xi принимают значения – 1 и +1 соответственно (принято обозначать – или +). Множество всех точек в k-мерном пространстве, координаты которых являются комбинациями "+" и "–", называется полным факторным планом или планом полного факторного эксперимента типа 2k (ПФЭ). Количество точек в этом плане N =2k.
Для примера возьмем полный факторный эксперимент с тремя независимыми переменными x1, х2и x3, табл. 3.1.
Второй, третий и четвертый столбцы таблицы соответствуют собственно плану экспериментов, пятый – восьмой столбцы содержит значения произведений независимых переменных. Фиктивная переменная x0 =1 (первый столбец) введена для единообразия записи расчетных формул коэффициентов полинома. Строки соответствуют опытам, например, первая строка характеризует эксперимент, в котором все независимые переменные находятся на нижнем уровне.
Таблица 3.1
| Матрица планирования | Вектор результатов | |||||||
| x0 | x1 | x2 | x3 | x1 x2 | x1 x3 | x2 x3 | x1 x2 x3 | y |
| + | – | – | – | + | + | + | – | y1 |
| + | – | – | + | + | – | – | + | y2 |
| + | – | + | – | – | + | – | + | y3 |
| + | – | + | + | – | – | + | – | y4 |
| + | + | – | – | – | – | + | + | y5 |
| + | + | – | + | – | + | – | – | y6 |
| + | + | + | – | + | – | – | – | y7 |
| + | + | + | + | + | + | + | + | y8 |
Существует несколько способов построения подобных матриц планирования. В частности можно воспользоваться приемом, характерным для записи последовательности двоичных чисел. В столбце последней переменной x3 знаки меняются поочередно, в столбце предпоследней переменной x2 – чередуются через два элемента, третьей справа переменной x1 – через четыре элемента. Аналогично строится матрица для любого количества переменных, порядок перечисления переменных не играет роли. Столбцы с произведениями переменных вычисляются путем умножения значений элементов в соответствующих столбцах простых переменных.
Из анализа матрицы планирования легко видеть, что полный факторный эксперимент обладает свойствами:
ортогональности. Сумма парных произведений элементов любых двух различных столбцов равна нулю. В частности, для простых переменных 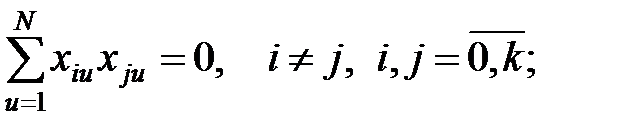
симметричности. Сумма всех элементов любого столбца, за исключением первого, равна нулю, например, 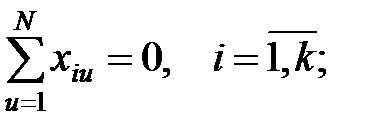
нормированности. Сумма квадратов элементов любого столбца равна числу опытов, так для i-й переменной 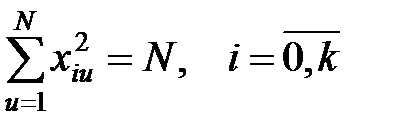 .
.
Первые два свойства обеспечивают независимость оценок коэффициентов модели и допустимость их физической интерпретации. Нарушение этих свойств приводит к взаимной зависимости оценок и невозможности придания смысла коэффициентам.
Включение в матрицу планирования переменных вида xi2 приведет к появлению единичных столбцов, совпадающих друг с другом и со столбцом x0. Следовательно, нельзя будет определить, за счет чего получено значение b0. Поэтому планы ПФЭ 2k не применимы для построения функции отклика в виде полного полинома второй степени.
Дата добавления: 2015-03-09; просмотров: 722;
