ВВЕДЕНИЕ. Важным фактором в повышении производительности труда инженеров и научных работников является автоматизация исследований
Важным фактором в повышении производительности труда инженеров и научных работников является автоматизация исследований, включающая в себя широкий круг задач — от моделирования творческого процесса, организации коллективов и планирования научных исследований на основе применения методов кибернетики до создания автоматизированных научных приборов, средств и систем автоматизации экспериментов. Однако все эти задачи неразрешимы без проведения экспериментов. Эксперимент занимает главенствующее место среди способов получения информации о внутренних взаимосвязях явлений в природе и технике. Он является отправной точкой и критерием большинства наших знаний. Экспериментальные поиски часто ведутся в таких областях, где теоретически нельзя сделать каких-либо предвидений. С помощью экспериментальных данных, получаемых непосредственно от изучаемых объектов, проверяется истинность теоретических предпосылок. Чтобы представить себе масштабы повседневной экспериментальной работы, достаточно наряду с натурными исследованиями, проводимыми в различных областях науки, при проектировании новой техники учесть также испытания образцов опытной и серийной продукции на тысячах заводов.
По мере роста сложности исследуемых процессов и явлений возрастают затраты на аппаратуру и проведение эксперимента. Для проведения некоторых специальных экспериментов требуется такое количество энергии, которое было бы достаточным для энергоснабжения города средней величины. При этом постоянно возрастает сложность решаемых задач, а большой объем информации, необходимой для выяснения внутренних взаимосвязей в природе и технике, заставляет применять все более сложные многомашинные комплексы для обработки информации (27, 67) все чаще оказываются недоступными непосредственному измерению Характеристики объектов испытаний, подлежащие определению в результате эксперимента. Вследствие этого совокупность технико-экономических показателей, по которым проводится оценка испытуемого объекта или принимаются важные организационные и инженерные решения, не совпадает, как правило, с совокупностью параметров объекта, определяемых по результатам натурного эксперимента. Важной задачей является организация испытаний объектов, процессы, функционирования которых носят сложный динамический характер и подвержены существенным влияниям изменяющихся условий внешней среды или динамических свойств человека. В ходе испытаний собирается большое количество экспериментальных данных, требующих обработки и анализа. Разработка технического объекта (или технологического процесса) в большинстве случаев включает следующие этапы: лабораторная установка — опытная установка — промышленная экспериментальная установка, хотя установки, построенные в лабораторных условиях, во многом допускают экстраполяцию на промышленные установки. При этом продолжительность анализа и осмысливания результатов испытаний и их учета для корректировки характеристик новых изделий весьма значительна. Этот процесс хорошо иллюстрируется в отечественной и зарубежной практике соотношением час испытаний — тысяча часов обработки [27, 30].
Широкое применение экспериментальных методов привело к созданию теории эксперимента. Эта теория призвана дать экспериментатору ответы ни следующие вопросы:
1) как нужно организовать эксперимент, чтобы наилучшим образом решить поставленную задачу (в смысле затрат времени и средств или точности результатов);
2) как следует обрабатывать результаты эксперимента, чтобы получить максимальное количество информации об исследуемом объекте (или явлении);
3) какие обоснованные выводы можно сделать об исследуемом объекте по результатам эксперимента.
ОБЩИЕ ПОЛОЖЕНИЯ ТЕОРИИ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТА
Основные понятия
Теория ПЭ охватывает практически все встречающиеся на практике варианты исследования объектов. В дальнейшем будут рассмотрены следующие типовые задачи экспериментального исследования:
поиск значений параметров системы, обеспечивающих достижение оптимального значения показателя качества исследуемого объекта при известных ограничениях на значения этих параметров. Перебор всех допустимых сочетаний значений параметров системы с целью поиска оптимального варианта нерационален по затратам ресурсов. Для решения указанной задачи ТПЭ предлагает такую последовательность проведения опытов, которая позволяет применить градиентные методы поиска при априорно неизвестной функции, связывающей показатель качества с параметрами системы;
приближенное аналитическое описание функциональной связи показателей качества с параметрами системы по результатам проведенного эксперимента. Традиционные методики проведения экспериментов из-за зависимости компонентов восстанавливаемого аналитического описания не позволяют определить раздельное влияние каждого фактора на результирующий показатель, т. е. эти методики обеспечивают получение аналитических зависимостей, пригодных лишь для решения интерполяционных задач. В отличие от них ТПЭ дает возможность оценить вклад каждого параметра в значение показателя, т.е. приближенно восстановить закон функционирования объекта по экспериментальным данным. Полученное аналитическое описание объекта можно использовать для предварительного исследования вариантов построения системы или в интересах построения модели старшей системы, включающей данный объект на правах элемента;
оценка дифференциального влияния уровней параметров системы на показатель качества. Такая задача возникает в случае, когда параметры системы являются по своей природе качественными или когда количественные параметры могут принимать небольшое число различных значений.
Кроме указанных, существуют и других задачи, решаемые с помощью ТПЭ, например:
испытания образцов техники. Планирование должно позволить оценить степень соответствия показателей качества образцов заданным требованиям при минимальном объеме испытаний;
отсеивающие эксперименты. Предназначены выявить параметры, незначительно влияющие на показатель качества системы. Соответствующие планы применяют на начальных этапах исследования, когда нет конкретных сведений о влиянии тех или иных параметров. Отсеивание несущественных факторов снижает трудоемкость решения задач оптимизации или приближенного аналитического описания системы;
адаптивное планирование. Применяется в условиях управления технологическим процессом, когда система управления все время должна приспосабливаться к конкретным условиям функционирования, а возможно, и предсказывать дальнейшее развитие процесса.
Решение задач с применением ТПЭ предусматривает использование априорной информации об изучаемом процессе для выбора общей последовательности управления экспериментами, которая уточняется после очередного этапа проведения исследований на основе вновь полученных сведений. Тем самым достигается возможность рационального управления экспериментами при неполном первоначальном знании характеристик исследуемого объекта. Целесообразность применения ТПЭ тем выше, чем сложнее исследуемая система.
В ТПЭ исследуемый объект (реальный объект, модель объекта) рассматривается как "черный ящик", имеющий входы v(управляемые независимые параметры) и выходы y[3, 6].
Переменные v принято называть факторами. Теория ПЭ изучает только активный тип экспериментов, когда имеется возможность независимо и целенаправленно менять значения факторов vво всем требуемом диапазоне. Факторы в эксперименте бывают качественными и количественными. Качественные факторы можно квантифицировать или приписать им числовые обозначения, тем самым перейти к количественным значениям. В дальнейшем будем считать, что все факторы являются количественными и представлены непрерывными величинами (если другое не оговорено особо). Переменным v можно сопоставить геометрическое понятие факторного пространства – пространства, координатные оси которого соответствуют значениям факторов. Совокупность конкретных значений всех факторов образует точку в многомерном факторном пространстве. Примерами факторов являются: интенсивность потока запросов к базе данных, скорость передачи данных по каналу, объем запоминающего устройств. Кроме того, на объект воздействуют возмущающие факторы, они являются случайными и не поддаются управлению.
Область планирования задается интервалами возможного изменения факторов vi min < vi < vi max для i =1, 2, …, k, где k – количество факторов. В теории ПЭ часто используют нормализацию факторов, т.е. преобразование натуральных значений факторов в безразмерные (кодированные) величины. Переход к безразмерным значениям xi задается преобразованием
| xi = (vi – vi0)/Dvi, | (1.1) |
где vi – натуральное значение фактора, vi0 – натуральное значение основного уровня фактора, соответствующее нулю в безразмерной шкале, Dvi – интервал варьирования. Совокупность основных уровней всех факторов представляет собой точку в пространстве параметров, называемую центральной точкой плана или центром эксперимента. С геометрической точки зрения нормализация факторов равноценна линейному преобразованию пространства факторов, при котором проводятся две операции: перенос начала координат в точку, соответствующую значениям основных уровней факторов; сжатие – растяжение пространства в направлении координатных осей.
Активный эксперимент включает: систему воздействий, при которых воспроизводится функционирование объекта; регистрацию отклика объекта. План эксперимента задает совокупность данных, определяющих количество, условия и порядок реализации опытов. Опыт составляет элементарную часть эксперимента и предусматривает воспроизведение исследуемого явления в конкретных условиях с последующей регистрацией результата. В условиях случайности в одних и тех же условиях проводятся параллельные (повторные) опыты в интересах получения статистически устойчивых результатов. Опыт u предполагает задание конкретных значений факторам v u = v1u, v2u, …, vku, а совокупность значений факторов во всех N точках плана эксперимента образует матрицу плана
| v11, v21, …, vk1 v12, v22, …, vk2 . . . . . v1N, v2N, …, vkN . | (1.2) |
Строки матрицы соответствуют опытам, столбцы – факторам, элемент матрицы viz задает значение z-го фактора в i-м опыте.
Вектор y называется откликом. В ТПЭ обычно изучается ситуация, в которой вектор отклика y состоит из одного элемента y. При наличии нескольких составляющих вектора y, каждую из них можно исследовать отдельно. Зависимость отклика от факторов носит название функции отклика, а геометрическое представление функции отклика– поверхности отклика. Функция отклика рассматривается как показатель качества или эффективности объекта. Этот показатель является функцией от параметров – факторов. На практике широкое распространение получили простые функции вида М{y'} = bf(v), где b=(b0, b1, …,bh) – вектор неизвестных параметров модели размерности h+1, f(v)=(f0(v), f1(v), …, fh(v)) – вектор заданных базисных функций, М{y'} – математическое ожидание функции отклика. Такое представление функции отклика соответствует линейной по параметрам модели регрессионного анализа, т.е. функция отклика есть линейная комбинация базисных функций от факторов.
Вследствие влияния на результаты экспериментов случайных воздействий истинные значения коэффициентов можно определить только приближенно. Оценку β= (β0, β1, …, βh)вектора неизвестных параметров b находят по результатам экспериментов, в ходе которых получают значения yu при заданных значениях факторов vu. Эти оценки обычно рассчитываются с помощью метода наименьших квадратов (МНК) на основе выборок значений факторов и откликов системы на воздействия [8]. В качестве оценки β вектора b выбирается такое значение, которое минимизирует 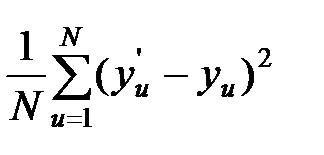 , где y'u – вычисленное на модели значение функции отклика в u-й точке факторного пространства. Приравнивая нулю частные производные от данной квадратичной формы, взятые по переменным b0, b1, …, bh, можно получить систему уравнений вида
, где y'u – вычисленное на модели значение функции отклика в u-й точке факторного пространства. Приравнивая нулю частные производные от данной квадратичной формы, взятые по переменным b0, b1, …, bh, можно получить систему уравнений вида 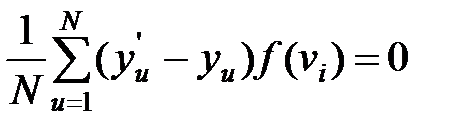 , где i= 0, 1, 2, …, h. Значение β находят путем решения этой системы уравнений. Решение системы возможно при линейной независимости базисных функций.
, где i= 0, 1, 2, …, h. Значение β находят путем решения этой системы уравнений. Решение системы возможно при линейной независимости базисных функций.
Если не принимать специальных мер, то оценки коэффициентовβ станут взаимозависимыми, и полученное выражение для функции отклика можно рассматривать только как интерполяционную формулу, что затрудняет ее физическую интерпретацию и последующие расчеты. Однако, формируя специальным образом матрицу плана, можно получить независимые значения β. И эти величины будут характеризовать вклад каждого фактора в значение функции отклика.
Итак, задача заключается в определении общей формы записи функции отклика y'. В большинстве случаев вид этой функции, получаемый из теоретических соображений, является сложным для практического применения, а при неполном знании объекта вообще неизвестен. По данным причинам функцию целесообразно представить в универсальном, удобном для практического применения виде, чему соответствует представление в виде полинома. Тогда системой базисных функций является совокупность степенных функций с целыми неотрицательными значениями показателей степени. Полиномиальная форма представления функции отклика примет вид
| y' = b0 + b1x1 + …+ bkxk + b12x1x2 + b13x1x3+… +bk–1,k xk–1xk + +b11x21 + … +bkkx2k + … + e, | (1.3) |
где e – случайная составляющая функции отклика (величина, характеризующая ошибку опыта).
Такая функция отклика линейна относительно неизвестных коэффициентов и будет полностью определена, если известны степень полинома и коэффициенты. Степень полинома задается исследователем априорно и уточняется в ходе исследования. На практике наибольшее распространение получили полиномы первого и второго порядка, соответственно линейные и квадратичные модели. Коэффициенты полинома принято называть эффектами факторов.
Иногда функцию отклика целесообразно представить в другом виде, например, в виде степенной функции, так как достижение заданной точности требует применения полинома высокого порядка. Однако использование функций, нелинейных относительно неизвестных параметров, усложняет вычисления, затрудняет оценку их свойств. В некоторых случаях задачу можно упростить путем искусственного преобразования нелинейной функции в линейную. При этом требуется соответствующее преобразование и результатов экспериментов.
Применение ТПЭ основано на ряде допущений, а именно [2, 6]:
функция отклика содержит в своем составе неслучайную и случайную составляющую. Многие показатели качества автоматизированных систем обработки информации носят случайный характер. Это требует многократного повторения опытов в одних и тех же условиях в целях получения статистически устойчивых результатов, а получаемые оценки показателей должны обладать свойствами состоятельности, эффективности, несмещенности и достаточности. Оценки типовых показателей формируются путем усреднения результатов наблюдений. Поэтому при достаточно большом количестве наблюдений можно считать, что случайная составляющая e распределена по нормальному закону с нулевым математическим ожиданием, что позволяет получить несмещенную оценку математического ожидания функции отклика в конкретной точке плана. Будем также считать, что величина e имеет дисперсию, не зависящую от значений факторов. Иначе говоря, результаты, полученные путем усреднения повторных опытов в каждой точке плана, представляют собой независимые, нормально распределенные случайные величины;
факторы v1, v2, …, vk измеряются с пренебрежимо малой ошибкой по сравнению с ошибкой в определении величины y (учет помех в задании факторов приводит к трудно разрешимым проблемам в оценке коэффициентов функции отклика). Ошибка в определении значения функции отклика объясняется не столько погрешностью измерений, сколько влиянием на результат работы системы неучтенных или случайных факторов, например различиями в формируемой последовательности случайных чисел при статистическом моделировании;
дисперсии среднего значения функции отклика в различных точках равны друг другу (выборочные оценки дисперсии однородны). Это означает, что при многократных повторных наблюдениях над величиной yu при некотором наборе значений v1u, v2u, …, vku, получаемая оценка дисперсии среднего значения не будет отличаться от оценки дисперсии, полученной при многократных наблюдениях для любого другого набора значений независимых переменных v1s, v2s, …, vks.
Указанные допущения позволяют использовать для расчетов коэффициентов полинома МНК, который дает эффективные и несмещенные оценки коэффициентов и обеспечивает простоту проведения самих расчетов. Применение МНК, вообще говоря, не требует соблюдения нормального распределения результатов наблюдения. Этот метод в любом случае дает решение, минимизирующее сумму квадратов отклонений результатов наблюдения от значений функции отклика. Допущение о нормальном распределении используется при проведении различного рода проверок, например, при проверке адекватности функции отклика и экспериментальных данных. Естественно, что точность оценок коэффициентов функции отклика повышается с увеличением числа опытов, по которым вычисляются коэффициенты.
Критерии оптимальности и типы планов
В настоящее время используется свыше 20 различных критериев оптимальности планов, которые подразделяются на две основные группы. К первой группе относят критерии, связанные с ошибками оценок коэффициентов, а ко второй – с ошибкой оценки поверхности отклика [2, 3, 6]. Далее будут охарактеризованы только те критерии, которые наиболее часто применяются при решении задач оптимизации, описания поверхности отклика и оценки влияния факторов.
Критерии первой группы представляют интерес для задач оптимизации, выделения доминирующих (наиболее значимых) параметров на начальных этапах решения оптимизационных задач или для выявления несущественных параметров в задачах восстановления закономерности функционирования объекта. Геометрическое истолкование свойств ошибок коэффициентов связано со свойствами эллипсоида их рассеяния, определяемого математическим ожиданием и дисперсией значений ошибок. Пространственное расположение, форма, и размер эллипсоида полностью зависят от плана эксперимента.
Критерию D-оптимальности соответствует минимальный объем эллипсоида рассеяния ошибок (минимум произведения всех дисперсий коэффициентов полинома). В соответствующем плане эффекты факторов максимально независимы друг от друга. Этот план минимизируют ожидаемую ошибку предсказания функции отклика. Критерию A-оптимальности соответствует план с минимальной суммарной дисперсией всех коэффициентов. Критерию E-оптимальности – план, в котором максимальная дисперсия коэффициентов будет минимальна.
Выбор критерия зависит от задачи исследования, так при изучении влияния отдельных факторов на поведение объекта применяют критерий Е-оптимальности, а при поиске оптимума функции отклика – D-оптимальности. Если построение D-оптимального плана вызывает затруднения, то можно перейти к А-оптимальному плану, построение которого осуществляется проще.
Критерии второй группы используются при решении задач описания поверхности отклика, определения ограничений на значения параметров. Основным здесь является критерий G-оптимальности, который позволяет построить план с минимальным значением наибольшей ошибки в описании функции отклика. Применение G-оптимального плана дает уверенность в том, что в области планирования нет точек с чрезмерно большой ошибкой описания функции.
Среди всех классов планов основное внимание в практической работе уделяется ортогональным и ротатабельным планам.
Ортогональным называется план, для которого выполняется условие парной ортогональности столбцов матрицы планирования, в частности, для независимых переменных 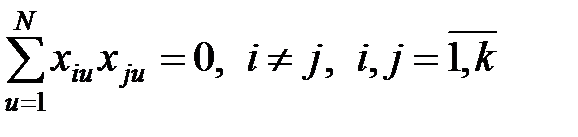 , где N – количество точек плана эксперимента, k – количество независимых факторов. При ортогональном планировании коэффициенты полинома определяются независимо друг от друга – вычеркивание или добавление слагаемых в функции отклика не изменяет значения остальных коэффициентов полинома. Для ортогональных планов эллипсоид рассеяния ориентирован в пространстве так, что направления его осей совпадают с направлениями координат пространства параметров.
, где N – количество точек плана эксперимента, k – количество независимых факторов. При ортогональном планировании коэффициенты полинома определяются независимо друг от друга – вычеркивание или добавление слагаемых в функции отклика не изменяет значения остальных коэффициентов полинома. Для ортогональных планов эллипсоид рассеяния ориентирован в пространстве так, что направления его осей совпадают с направлениями координат пространства параметров.
Использование ротатабельных планов обеспечивает для любого направления от центра эксперимента равнозначность точности оценки функции отклика (постоянство дисперсии предсказания) на равных расстояниях от центра эксперимента. Это особенно важно при решении задач поиска оптимальных значений параметров на основе градиентного метода, так как исследователь до начала экспериментов не знает направление градиента и поэтому стремится принять план, точность которого одинакова во всех направлениях. В ряде случаев при исследовании поверхности отклика требуется униморфность модели, а именно, соблюдение постоянства значений дисперсии ошибки в некоторой области вокруг центра эксперимента. Выполнение такого требования целесообразно в тех случаях, когда исследователь не знает точно расположение области поверхности отклика с оптимальными значениями параметров. Указанная область будет определена на основе упрощенной модели, полученной по результатам экспериментов.
По соотношению между количеством оцениваемых неизвестных параметров модели и количеством точек плана эксперимента все планы подразделяются на три класса: ненасыщенные – количество параметров меньше числа точек плана; насыщенные – обе величины одинаковы; сверхнасыщенные – количество параметров больше числа точек плана. Метод наименьших квадратов применяют только при ненасыщенном и насыщенном планировании, и он не применим для сверхнасыщенного планирования.
Для некоторых планов важную роль играет свойство композиционности. Так, композиционные планы для построения полиномов второго порядка получают добавлением некоторых точек к планам формирования линейных функций. Это дает возможность в задачах исследования сначала попытаться построить линейную модель, а затем при необходимости, добавив наблюдения, перейти к моделям второго порядка, использую ранее полученные результаты и сохраняя при этом некоторое заданное свойство плана, например его ортогональность.
Между критериями оптимальности и методами построения оптимальных планов экспериментов существует жесткая связь. Построение планов производится или с использованием каталогов планов или с использованием непосредственно методов планирования экспериментов, что является непростой задачей и требует достаточно высокой квалификации исследователя в области ТПЭ.
Кроме рассмотренных критериев в планировании экспериментов вполне естественно применяется критерий минимума числа экспериментов, т.е. среди всех планов желательно выбирать такой, который требует минимального числа опытов при соблюдении требований к качеству оценки функции или ее параметров.
Как было отмечено выше, одной из областей применения ТПЭ является решение задач оптимизации, причем непосредственно для поиска оптимальных решений используются градиентные методы. Вычисление оценки градиента осуществляется на основе обработки экспериментальных данных. Хотя градиентный метод оптимизации не является составной частью ТПЭ, в целях удобства освоения материала далее приведено его краткое изложение.
Дата добавления: 2015-03-09; просмотров: 900;
