Поток освобождения серверов

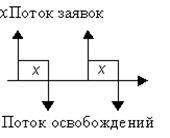Пусть x_k –длительность обслуживания k –ой заявки. При детерминированном характере обслуживания задается набор этих значений. При x = x_k время обслуживания постоянно и поток освобождения совпадает по характеристикам с потоком заявок. При случайном характере обслуживания задают вероятность того, что обслуживание займет время меньшее, чем x: .

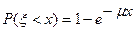Рис. 2, на котором показаны результаты экспериментального измерения времени занятия абонентской линии на АТС подтверждает практическую приемлемость такой аппроксимации.

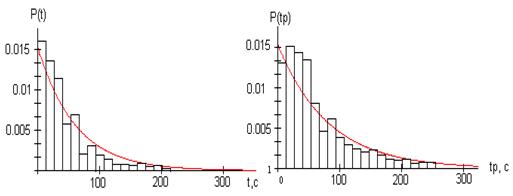
Рис. 2. Гистограммы измерений длительности занятий при x = 60,3 с, s = 84,4 и разговоров при x = 81,2 с, s = 90,1

Если освободившийся сервер сразу же занимается новым обслуживанием, то отношение 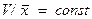, где V – общее число серверов, а 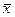– среднее время обслуживания. Вероятность того, что за промежуток времени t произойдет i освобождений, будет равна:

.

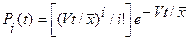В более общем случае, когда занято k серверов, вероятность освобождения i серверов за время t при показательном законе распределения времени обслуживания получим

.

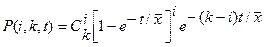Вероятность того, что не освободится ни один сервер: .

Параметр потока освобождений при занятии k серверов можно найти как предел

.

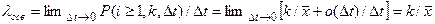Поток освобождений ординарный и его параметр пропорционален числу занятых серверов. Коэффициент пропорциональности – величина обратная среднему времени обслуживания.

СРС 2 по дисциплине “Теория распределение информации»

Наименование темы: Классификация систем массового обслуживания. Формула Литтла