Поток Эрланга
Частный случай и получается “просеиванием” потока Пальма. Если отбрасывать каждую вторую заявку – то получается поток Эрланга второго порядка, если каждую третью – третьего порядка и т.д.
Простейший пуассоновский поток можно рассматривать как поток Эрланга первого порядка. Обозначим pn(t) плотность вероятности промежутка между заявками. Можно получить что: 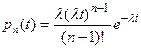 .
.
Закон распределения для потока Эрланга n-го порядка:
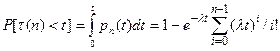 ,
,
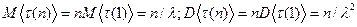 .
.
Нормируем масштаб времени так, чтобы параметр потока не зависел от n .
Τн (n)=τ(n)/n ; интенсивность Λn
Нормированный поток Эрланга n – го порядка:
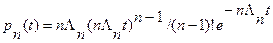
Обобщенный поток Эрланга n –го порядка .
Если τ(n) есть сумма случайных величин, каждая из которых распределена по показательному закону с параметром λi
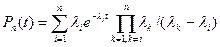 ,
,
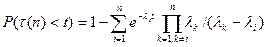 ,
,
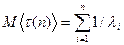 ,
,  .
.
Дата добавления: 2015-03-07; просмотров: 779;
