Теоретическое описание
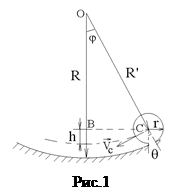 Радиус кривизны R гладкой сферической поверхности можно определить, измерив период колебания Т шарика, катающегося по этой поверхности.
Радиус кривизны R гладкой сферической поверхности можно определить, измерив период колебания Т шарика, катающегося по этой поверхности.
Если пренебречь потерями энергии, затрачиваемой на преодоление диссипативной силы трения, то для катающегося без проскальзывания шарика должен выполняться закон сохранения механической энергии. Центр масс C шарика движется поступательно, но, кроме того, шарик вращается относительно оси z, проходящей через точку C перпендикулярно плоскости (рис.1). Поэтому полная механическая энергия шарика
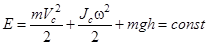 (1)
(1)
|
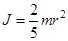 - его момент инерции относительно оси z; r – радиус шарика.
- его момент инерции относительно оси z; r – радиус шарика.
Модуль угловой скорости w шарика вокруг оси z связан с модулем скорости Vc поступательного движения центра масс соотношением
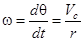 . (2)
. (2)
Подставляя (2) и выражение для Jc в (1), получаем
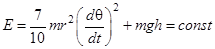 . (3)
. (3)
Но при качении шарика по сферической поверхности его центр масс отклоняется относительно центра O поверхности на угол j. Из рис.1 видно, что угол j связан с углом поворота q шарика относительно оси z соотношением
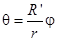 (4)
(4)
где 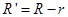 . Кроме того, из прямоугольного треугольника ОВС следует, что
. Кроме того, из прямоугольного треугольника ОВС следует, что
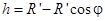 . (5)
. (5)
Подставляя (4) и (5) в формулу (3), выражаем полную механическую энергию шарика через угол j:
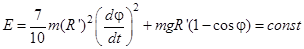 . (6)
. (6)
В верхней точке траектории скорость шарика равна нулю и вся механическая энергия шарика переходит в потенциальную. При прохождении шариком положения равновесия (h=0) скорость и кинетическая энергия шарика максимальны.
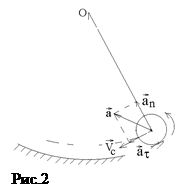
Рассмотрим кинематику движения шарика. Скорость 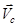 его центра масс С всегда направлена по касательной к траектории (рис.2). Полное ускорение
его центра масс С всегда направлена по касательной к траектории (рис.2). Полное ускорение 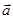 центра масс равно сумме тангенциального
центра масс равно сумме тангенциального 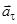 и нормального
и нормального 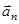 ускорений. Ускорение
ускорений. Ускорение 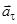 направлено также по касательной к траектории. Его модуль связан с модулем углового ускорения вращения шарика вокруг оси z формулой
направлено также по касательной к траектории. Его модуль связан с модулем углового ускорения вращения шарика вокруг оси z формулой
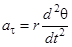 . (7)
. (7)
Ускорение 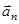 направлено к центру кривизны. Его модуль
направлено к центру кривизны. Его модуль
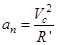 . (8)
. (8)
Эти модули изменяются при колебательных движениях шарика периодически. В верхней точке траектории при наибольшем отклонении шарика от положения равновесия Vc шарика и an равны нулю, а ar достигает максимума. При прохождении положения равновесия, наоборот, 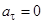 , а Vc и an максимальны.
, а Vc и an максимальны.
Найдем период колебаний шарика. Для этого необходимо получить динамическое уравнение колебаний (т.е. уравнение динамики для поступательного или вращательного движения колеблющегося шарика).Для любых незатухающих гармонических колебаний это уравнение имеет общий вид
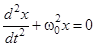 . (9)
. (9)
Физическое тело будет совершать гармонические колебания в том случае, если на него действует сила или момент силы, пропорциональные смещению от положения равновесия и стремящиеся вернуть тело в положение равновесия.
Воспользуемся законом сохранения механической энергии (6). Возьмем производную по времени от обеих частей этого уравнения, сократим полученное выражение на 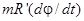 и приведем его к виду, аналогичному (9):
и приведем его к виду, аналогичному (9):
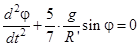 . (10)
. (10)
Отсюда видно, что шарик будет совершать гармонические колебания относительно положения равновесия в том случае, когда 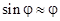 . Т.е. условием гармонических колебаний в данной работе будут малые углы отклонения шарика от положения равновесия.
. Т.е. условием гармонических колебаний в данной работе будут малые углы отклонения шарика от положения равновесия.
В этом случае угол j изменяется по гармоническому закону 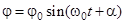 , где
, где
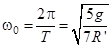 . (11)
. (11)
Используя выражения (4), (7) и (8), можно вычислить значения скорости и ускорения шарика в любой момент времени. Чтобы найти зависимость радиуса кривизны R сферической поверхности от периода T, которую находим из формулы (11), подставим в нее 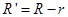 :
:
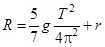 . (12)
. (12)
При вычислении мы не учитывали, что механическая энергия шарика уменьшается за счет работы диссипативной силы трения и потому в действительности колебания шарика будут затухающими. Затуханием колебаний в работе пренебрегаем.
Дата добавления: 2015-03-07; просмотров: 952;
