Порядок выполнения работы. 1. Измерить линейкой радиусы дисков R и r, а также длину нити l
1. Измерить линейкой радиусы дисков R и r, а также длину нити l. Занести данные в Таблицу 1.
2. Резко повернуть рукой диск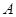 
до упора и отпустить. При этом нижний диск В должен совершать крутильные колебания, а верхний диск А должен остаться в покое из-за трения в оси.
3. С помощью секундомера определить время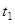 
полных n =20 колебаний ненагруженного диска. Опыт повторить три раза. Вычислить среднее значение 
и среднее значение периода колебаний 
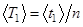. Результаты измерений и вычислений занести в таблицу 1.
Таблица 1.
| m1, кг | R, м | r, м | l, м | t1, с | ,с
| <T1>, с |
4. Положить на нижний диск исследуемое тело так, чтобы центры масс тела и диска были на одной оси. Масса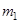 
диска В имасса исследуемого тела m2 указаны на установке.
5. Определить время 
полных n=20 колебаний нагруженного диска. Опыт повторить три раза. Вычислить среднее значение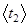 
и среднее значение периода колебаний 
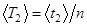. Результаты измерений и вычислений занести в таблицу 2.
6. Используя экспериментальные данные, вычислить момент инерции Iэксп исследуемого тела по формуле
.
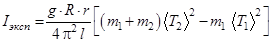7. Измерить размеры исследуемого тела и из таблицы 3 для данной формы тела вычислить теоретический момент инерции Iтеор тела относительно той же оси, что и при эксперименте.
Содержание отчета
Сравнить теоретическое Iтеор и экспериментальное Iэксп значения момента инерции. Для этого вычислить относительное отклонение 
от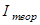 
по формуле 
С пункта 3 по 8 проделать аналогично измерения и вычисления с другими телами .
Таблица 2.
| Вид тела и его размеры | m2, кг | t2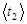, с |  ,
с
| <T2>, с | Iэксп, кг×м2 | Iтеор, кг×м2 | Iэксп – Iтеор, кг×м2 |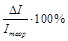 
|
| Диск R = м | ||||||||
| Прямоугольник a = м b = м | ||||||||
| Треугольник a = м | ||||||||
Таблица 3. Моменты инерции плоских тел относительно оси, проходящей через центр масс перпендикулярно их плоскости.
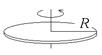
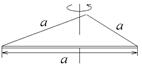
Диск Прямоугольник Равностор. треугольник
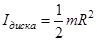
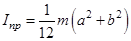
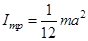
Дата добавления: 2015-03-07; просмотров: 683;