Момент инерции плоской треугольной пластины относительно оси, проходящей через центр масс перпендикулярно ее плоскости.
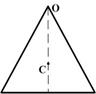
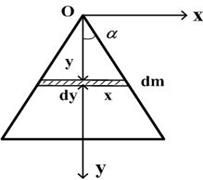 Разобьем пластину на тонкие стержни массой dm длиной 2x и высотой dy, как показано на рисунке. Так как для стержня длины
Разобьем пластину на тонкие стержни массой dm длиной 2x и высотой dy, как показано на рисунке. Так как для стержня длины 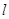 момент инерции относительно перпендикулярной оси, проходящей через центр масс равен
момент инерции относительно перпендикулярной оси, проходящей через центр масс равен 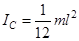 , то момент инерции такого стержня относительно оси, проходящей через точку О перпендикулярно плоскости чертежа, по теореме Штейнера , равен:
, то момент инерции такого стержня относительно оси, проходящей через точку О перпендикулярно плоскости чертежа, по теореме Штейнера , равен:
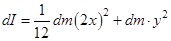 ,
,
где массу стержня 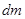 можно выразить из пропорции
можно выразить из пропорции
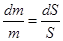 ,
,
где 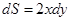 – площадь стержня, а
– площадь стержня, а 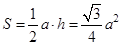 – площадь равностороннего треугольника.
– площадь равностороннего треугольника.
Тогда масса стержня: 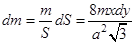 , а его момент инерции:
, а его момент инерции: 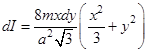
С учетом того, что для равностороннего треугольника 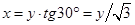 , получим:
, получим: 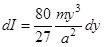
 Тогда
Тогда 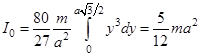 . Но по теореме Штейнера
. Но по теореме Штейнера 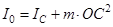 , тогда, учитывая, что
, тогда, учитывая, что 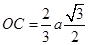 , получим выражение для
, получим выражение для 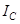 :
:
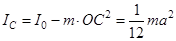
Дата добавления: 2015-03-07; просмотров: 2796;
