Теоретическое описание. На любое движущееся тело действуют силы трения.

На любое движущееся тело действуют силы трения.

Внешним (сухим) трением называют явление, заключающееся в возникновении касательных сил, препятствующих относительному перемещению тел, в месте контакта этих тел. Если тела неподвижны друг относительно друга, то говорят о трении покоя; при их относительном перемещении говорят о трении скольжения.

Г.Амонтон и Ш.Кулон установили опытным путем закон статического трения: Предельное значение силы статического трения прямо пропорционально значению силы нормального давления тела на опору, т.е.

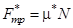; (1)

где μ* – коэффициент статического трения; μ* зависит от материала и состояния поверхности соприкасающихся тел.

Для трения скольжения закон Амонтона-Кулона записывается аналогично (1):

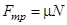(2)

где μ – коэффициент трения скольжения.

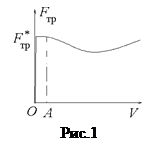При малых скоростях на малом интервале ОА сила трения приближенно постоянна, затем уменьшается, достигает минимума и начинает возрастать (рис.1). Строгой теории сил трения еще нет, но можно дать следующее объяснение возникновению сил трения.

На поверхностях тела и поверхности имеются отдельные выступы, за которые они цепляются. При зацеплении их существенную роль играют силы молекулярного притяжения. Соприкосновение тел происходит в действительности на отдельных участках. Их общая площадь значительно меньше видимой площади соприкосновения. На этих участках создаются высокие местные давления, которые вызывают деформации поверхностного слоя и взаимное внедрение отдельных микрочастей тел.

При действии сил трения скольжения всегда происходит превращение механической энергии во внутреннюю, в результате тела нагреваются. Силу трения поэтому называют диссипативной. Работа силы трения по любому пути обычно отрицательная (A_тр < 0).

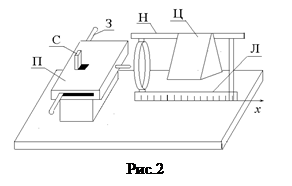
Для определения силы трения скольжения в данной работе применимы законы сохранения импульса и изменения механической энергии при неупругом соударении пули с цилиндром. При выстреле из пружинного пистолета П пуля попадает в цилиндр Ц, перемещаясь с ним по направляющей Н (рис.2). По шкале линейки Л определяется величина перемещения цилиндра с пулей при действии силы трения скольжения в месте контакта цилиндра с направляющей.

Рассмотрим систему "пуля-цилиндр". В направлении выстрела (ось х) сохраняется проекция импульса этой системы, т.е.

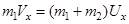(3)

где m₁ и m₂ – массы пули и цилиндра соответственно; V_x и U_x – проекции скоростей пули до удара и системы после удара пули соответственно.

На систему "пуля-цилиндр" после удара действует сила трения скольжения. Учитывая, что потенциальная энергия этой системы не изменяется, применяем закон изменения механической энергии:

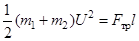, (4)

где F_трl – абсолютное значение работы силы трения скольжения при перемещении цилиндра с пулей на расстояние l.

Аналогично имеем для системы "пружина-затвор-пуля":

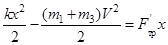, (5)

где k – коэффициент упругости; х – деформация пружины; m₃ – масса затвора (затвор остается в стволе); F'_тр – абсолютное значение работы силы трения при перемещении затвора с пулей в стволе на пути х (ввиду ее малости принимаем равной нулю).

Из (3), (4) и (5) получаем

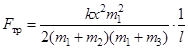. (6)

Примечание. Величины k, m₁, m₂ указаны на установке;

а так как m₃ ≈ 0, то формулу (6) можно упростить

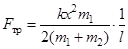(7)