Определение моментов инерции методом колебаний

Цель работы: экспериментально определить момент инерции однородного стержня относительно двух параллельных осей, результат сопоставить с теоремой Штейнера.

Теоретическое описание

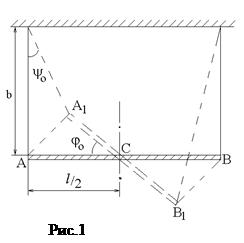
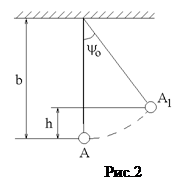
В данной работе методом колебаний определяем моменты инерции стержня относительно оси, проходящей через центр масс, J_c, и относительно параллельной ей оси, проходящей через конец стержня, J_A. Для определения момента инерции J_c наблюдаем малые колебания стержня на бифилярном подвесе (рис.1,2). Для определения момента инерции стержня J_A наблюдаем малые колебания, подвесив его за конец (рис.3).

За счет трения в точках подвеса энергия колебаний стержня уменьшается. Однако если ограничится наблюдением нескольких колебаний (в пределах 10-20 колебаний), то работа сил трения будет невелика, Ее можно не учитывать и при малых углах отклонения (6-8°) колебания считать гармоническими:

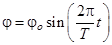(1)

где j₀ – угловая амплитуда; T – период колебаний. Так как работой сил трения пренебрегаем, то полная механическая энергия стержня остается неизменной. При прохождении положения равновесия стержень обладает только кинетической энергией: 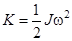, где w – максимальная угловая скорость.

При отклонении стержня от положения равновесия на максимальный угол его полная механическая энергия (потенциальная) U = mgh, где h – максимальная высота поднятия центра масс стержня.

Запишем закон сохранения энергии

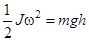(2)

Формулы (1) и (2) позволяют найти момент инерции J, если измерен на опыте период колебаний T.

1. Определение J_c – момента инерции стержня относительно оси симметрии.

Стержень на бифилярном подвесе совершает крутильные колебания (см. рис.1). Определяем его максимальную угловую скорость w, продифференцировав (1) по времени:

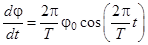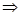
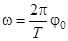; (3)

Максимальная высота подъема центра масс стержня определяется углом ψ₀ (см.рис.2):

,

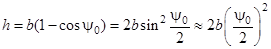где b – длина нити подвеса; ψ₀ – максимальный угол отклонения нити, однозначно связанный с максимальным углом отклонения стержня от положения равновесия j₀. При малых значениях j₀ и ψ₀ конец стержня проходит путь AA₁, который приближенно можно считать равным длине дуги AA₁:

, .

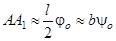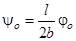Теперь выразим h через угол φ_o:

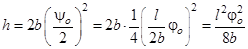(4)

Подставляя (3) и (4) в (2), получаем

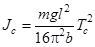(5)

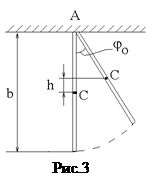2. Определение J_A момента инерции стержня относительно оси, перпендикулярной ему и проходящей через конец.

В формулу (2) подставляем соответствующие значения максимальной скорости при прохождении положения равновесия w из (3) и максимальной высоты поднятия центра масс h (рис.3). Из рис.3 получаем связь между h и углом j₀:

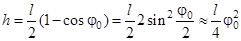(6)

Из равенства (20) с учетом (3) и (6) получаем

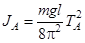(7)

Таким образом, измеряя на опыте периоды колебаний стержня T_c и T_A, длину нити подвеса, длину стержня, можно вычислить моменты инерции J_c и J_A стержня относительно параллельных осей, а результат сопоставить с теоремой Штейнера.