Лабораторная работа № 3

СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ ДЛЯ ФОТОНОВ

Теоретическая часть

Соотношение неопределенностей (принцип неопределенности) – фундаментальное положение квантовой теории, утверждающее, что любая физическая система не может находиться в состояниях, в которых координаты ее центра инерции и импульс одновременно принимают вполне определенные, точные значения.

Принцип неопределенности, открытый в 1927 году немецким физиком В. Гейзенбергом, явился важным этапом в выяснении закономерностей внутриатомных явлений и построении квантовой механики. Существенной чертой микроскопических объектов является их корпускулярно-волновая природа. Состояние частиц полностью определяется волновой функцией. Частица может быть обнаружена в любой точке пространства, в которой волновая функция отлична от нуля. Поэтому результаты экспериментов по определению, например, координаты микрочастицы имеют вероятностный характер.

Количественно соотношение неопределенностей формулируется следующим образом. Если Dх – неопределенность значения координаты х центра инерции системы, а Dр_х – неопределенность проекции импульса 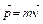на ось х, то произведение этих неопределенностей должно быть по порядку величины не меньше постоянной Планка ћ = h/2p. Аналогичные неравенства должны выполняться для любой пары так называемых канонически сопряженных переменных, например: для координаты у и проекции импульса р_у на ось y, координаты z и проекции импульса p_z на ось Z. Если под неопределенностями координаты и импульса понимать среднеквадратичные отклонения этих величин от их средних значений, то соотношения неопределенностей имеют вид:

Dр_х × Dх ³ ћ,

Dр_y × Dу ³ ћ, (3.1)

Dр_Zx × Dz ³ ћ.

Ввиду малости ћ (ћ = 1,05 × 10^–34 Дж × с) по сравнению с макроскопическими величинами той же размерности, соотношения неопределенностей существенны в основном для явлений атомных (и меньших) масштабов и не проявляются в опытах с макроскопическими телами.

Из соотношений неопределенностей следует, что чем точнее определена одна из входящих в неравенство величин, тем менее точно определено значение другой. Никакой эксперимент не может привести к одновременно точному измерению таких динамических переменных; при этом неопределенность в измерениях связана не с несовершенством экспериментальной техники, а с объективными свойствами материи.

Соотношение неопределенностей было установлено из рассмотрения, в частности, следующего примера. Пусть плоская световая волна Е = Е₀ × соs(wt – kz + j) падает на щель шириной Dх (рис. 3.1) и распространяется вдоль оси z.

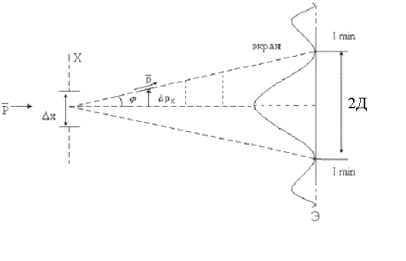
Рис. 3.1

После щели световые волны распространяются во всевозможных направлениях, т.е. на экране наблюдается явление дифракции. Дифракционная картина, наблюдаемая на экране Э, характеризуется главным (центральным) максимумом, расположенным симметрично относительно оси Z, и побочными максимумами по обе стороны от главного (максимумами высших порядков можно пренебречь, поскольку их интенсивность мала по сравнению с интенсивностью центрального максимума).

До прохождения фотона через щель, его импульс равен 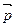(если представить световую волну как поток фотонов), а составляющая импульса р_х = 0 (щель перпендикулярна к импульсу), так что Dр_х = 0, зато координата х частицы является совершенно неопределенной. Если значение компоненты импульса частицы определено, то соответствующая компонента координаты полностью неопределенна. В момент прохождения фотона через щель положение меняется. Вместо полной неопределенности координаты х появляется неопределенность Dх, но это достигается ценой утраты определенности значения р_х. Вследствие дифракции фотоны отклоняются от первоначального направления и будут двигаться в пределах ограниченного угла 2j, где j – угол, соответствующий первому дифракционному минимуму. Таким образом, появляется неопределенность в значении составляющей импульса вдоль оси х. Из рис. 3.1(из треугольника) следует:

Dр_х = р × sin j. (3.2)

Из теории дифракции для одной щели известно, что положение первого дифракционного минимума соответствует условию:

Dх × sin j = kl, где k=1 (3.3)

где l – длина волны фотона,

Dх – ширина щели.

φ- угол дифракции.

k – порядок min

Учитывая, что импульс фотона определяется формулой де Бройля р = h/l, из формул (3.2) и (3.3) получим

Dр_х × Dх = ћ. (3.4)

Но для некоторой, хотя и незначительной, части фотонов, попадающих за пределы центрального максимума, величина Dр_х ³ р × sin j. Для общего случая получается соотношение:

Dр_х × Dх ³ , 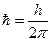(3.5)

В данной работе соотношение неопределенностей (3.5) проверяется экспериментально для фотонов. На опыте измеряется ширина щели Dх, которая характеризует неопределенность координаты фотона в направлении х, и ширина главного центрального - фракционного max 2Д, характеризующая неопределенность значения поперечной составляющей импульса фотона Dр_х.

Описание экспериментальной установки

Установка для проверки соотношения неопределенностей (рис. 3.2) состоит из гелий-неонового лазера (1) (источник монохроматического света l = 632,8 нм), регулируемой щели (2) и экрана (3) (на нем наблюдается дифракционная картина), которые укреплены на оптической скамье. Испускаемый лазером (1) пучок света проходит через калиброванную щель (2) и попадает на экран (3), в качестве которого используется лист миллиметровой бумаги.

1 2 3

Лазер Регулируемая щель Экран

Рис. 3.2