Оценка точности прямых многократных измерений
Пусть при повторении измерений физической величины 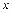 в одинаковых условиях получили некоторые различные значения:
в одинаковых условиях получили некоторые различные значения: 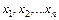 (n – число измерений). Это означает, что за наиболее достоверное значение измеряемой величины
(n – число измерений). Это означает, что за наиболее достоверное значение измеряемой величины 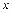 принимают среднее арифметическое
принимают среднее арифметическое 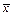 из всех n результатов измерений:
из всех n результатов измерений:
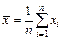 . (2)
. (2)
Окончательный результат измерения величины 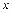 представляют в виде:
представляют в виде:
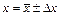 , (3)
, (3)
где 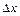 – положительная величина, называемая абсолютной погрешностью найденной величины
– положительная величина, называемая абсолютной погрешностью найденной величины 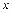 . Доверительной вероятностью
. Доверительной вероятностью 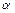 (надёжностью) полученного результата измерения физической величины
(надёжностью) полученного результата измерения физической величины 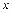 называется вероятность
называется вероятность 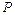 того, что истинное значение
того, что истинное значение 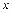 действительно лежит в интервале от
действительно лежит в интервале от 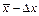 до
до 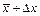 . А соответствующий этому значению
. А соответствующий этому значению 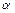 интервал
интервал 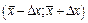 – доверительным интервалом. При большом числе измерений полуширина доверительного интервала при заданном значении
– доверительным интервалом. При большом числе измерений полуширина доверительного интервала при заданном значении 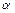 равна:
равна:
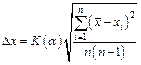 , (4)
, (4)
где 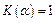 при
при 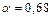 ;
; 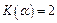 при
при 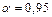 ;
; 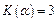 при
при 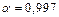 . При малом числе измерений,
. При малом числе измерений, 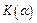 зависит не только от доверительной вероятности
зависит не только от доверительной вероятности 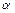 , но и от числа измерений
, но и от числа измерений 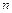 . Поэтому, если систематическими погрешностями можно пренебречь, то абсолютная погрешность (полуширина доверительного интервала) находится по формуле:
. Поэтому, если систематическими погрешностями можно пренебречь, то абсолютная погрешность (полуширина доверительного интервала) находится по формуле:
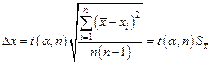 , (5)
, (5)
где: 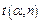 – коэффициент Стьюдента. Для
– коэффициент Стьюдента. Для 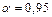 , принятой в студенческом лабораторном практикуме, значения
, принятой в студенческом лабораторном практикуме, значения 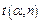 таковы:
таковы:
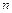
| ¥ | |||||||||
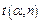
| 4.3 | 3.2 | 2.8 | 2.6 | 2.5 | 2.4 | 2.3 | 2.3 |
Величину 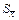 называют среднеквадратичной погрешностью среднего арифметического из серии измерений.
называют среднеквадратичной погрешностью среднего арифметического из серии измерений.
В общем случае необходимо принимать во внимание как случайные, так и систематические погрешности измеряемых величин. Погрешность прибора обычно указывается в его паспорте или условным знаком на шкале прибора. Обычно под погрешностью прибора 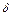 понимают полуширину интервала, внутри которого с доверительной вероятностью
понимают полуширину интервала, внутри которого с доверительной вероятностью 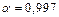 может быть заключена измеряемая величина. Это верно в том случае, если погрешность измерений обусловлена только погрешностью прибора. В качестве полной погрешности результата измерений с доверительной вероятность
может быть заключена измеряемая величина. Это верно в том случае, если погрешность измерений обусловлена только погрешностью прибора. В качестве полной погрешности результата измерений с доверительной вероятность 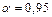 примем:
примем:
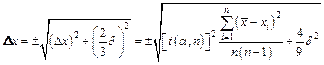 . (6)
. (6)
Абсолютная погрешность позволяет установить, в каком знаке полученного результата содержится неточность. Относительная погрешность дает информацию о том, какую долю (процент) измеряемой величины составляет абсолютная погрешность. Окончательный результат серии прямых измерений величины 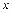 записывают в виде:
записывают в виде:
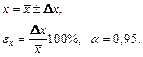 (7)
(7)
Таким образом, любая физическая величина, найденная опытным путем должна быть представлена: средним значением 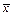 ; доверительной вероятностью
; доверительной вероятностью 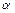 ; абсолютной погрешностью (полушириной доверительного интервала)
; абсолютной погрешностью (полушириной доверительного интервала) 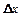 ; относительной погрешностью
; относительной погрешностью 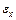 .
.
Дата добавления: 2015-03-03; просмотров: 747;
