Существо концепции детерминизма. Понятие состояния

В п. 1.7.6.4 отмечалось, что механической картине мира свойствен детерминизм, то есть представление о полной предопределенности будущего. Это представление основано на том математическом факте, что уравнения механики, описывающие движение тела, при условии, что для какого-нибудь момента времени заданы положение и скорость этого тела (начальные условия), имеют единственное решение. Отыскав его, мы сможем сказать, где тело находилось в любой момент прошлого, и где оно будет находиться в любой будущий момент.

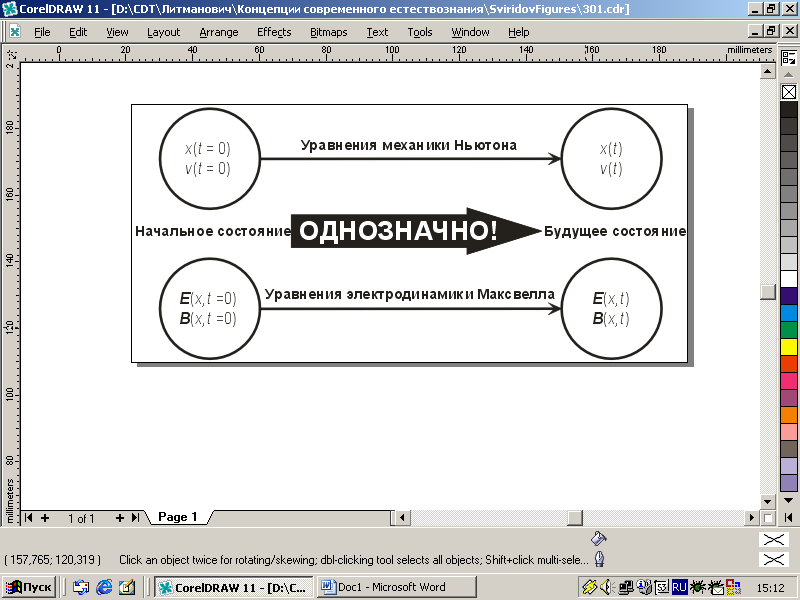В механической картине мира впервые оформилось понятие состояния физической системы. В наиболее общей формулировке, состояние системы — это совокупность данных, позволяющая предсказать эволюцию системы во времени.

В механике состояние системы описывается значениями физических величин — координат и скоростей тел, входящих в систему. Законы механики позволяют, в принципе, по начальному состоянию системы однозначно

определить значения физических величин, определяющих ее состояние, для любого будущего или прошлого момента времени. Тем же свойством обладают уравнения электродинамики Максвелла, с той лишь разницей, что в ней состояние системы определяется не координатами и скоростями частиц, а значениями электрического и магнитного полей в каждой точке пространства. Поэтому детерминизм так же свойствен электромагнитной картине мира, как и механической. Однако тот же Максвелл стал одним из создателей теории, продемонстрировавшей несостоятельность механического детерминизма — молекулярно-ки­не­ти­чес­кой теории газов.

3.4.2. Молекулярно-кинетическая теория: неизбежность случайности

Первоначально основная идея молекулярно-кинетической теории (МКТ) заключалась в том, чтобы, рассмотрев механическое движение молекул газа, теоретически вывести законы термодинамики, установленные опытным путем. Главная трудность на этом пути — огромное число молекул в любой представляющей интерес системе, обычно соизмеримое с числом Авогадро, N_A = 6×10²³. Совершенно нереально даже записать уравнения движения для каждой из такого количества молекул, не говоря уже о том, чтобы решить. Поэтому Максвеллу пришлось изменить саму постановку задачи. Вместо того чтобы искать, каковы в точности положение и скорость данной молекулы, он задался вопросом, какова вероятность того, что скорость молекулы имеет определенное значение. Оказалось, что ответ на этот вопрос — знаменитое распределение Максвелла молекул по скоростям — несложно получить, не вдаваясь в детали взаимодействия молекул друг с другом.

Поначалу Максвелл полагал, что использование вероятностей является лишь техническим приемом, позволяющим упростить решение трудной задачи. Однако в ходе исследований он пришел к убеждению, что в системах большого числа частиц присутствует элемент случайности, который принципиально не может быть учтен в рамках механической, детерминированной схемы. Аналогичную эволюцию претерпели взгляды другого выдающегося физика XIX века, Людвига Больцмана. Начав с

попыток вывести законы термодинамики из ньютоновской механики молекул, он пришел к пониманию того, что поведение больших коллективов частиц управляется более глубокими законами — не механическими, а вероятностными. Пример, которым Больцман пояснял, почему бессмысленно говорить о детерминированности траекторий молекул, можно изложить следующим образом.

В 30-литровой фляге из тех, в которых перевозят молоко или сметану, при нормальных атмосферных условиях содержится около 10²⁴ молекул воздуха. Вообразим, что с помощью некоего чудесного компьютера мы рассчитали траекторию будущего движения каждой молекулы. Теперь удалим из фляги одну-един­ст­вен­ную молекулу. Сильно ли это повлияет на движение остальных 99999999999999999999999 молекул? На первый взгляд, почти не повлияет. Однако разберемся внимательнее.

Совершая тепловое движение, молекулы сталкиваются друг с другом, изменяя при этом направление и величину своей скорости. При нормальных условиях каждая молекула воздуха испытывает около миллиарда столкновений ежесекундно. Поэтому уже через одну миллиардную долю секунды после удаления молекулы из фляги, там появится одна молекула, траектория движения которой существенно изменилась, — та, с которой должна была столкнуться удаленная молекула. Спустя две миллиардных доли секунды таких молекул станет четыре:

- та, с которой должна была столкнуться удаленная;

- та, которая уже изменила свою траекторию;

- та, с которой не столкнулась молекула, изменившая траекторию,

- и, наконец, та, с которой она столкнулась.

Спустя еще миллиардную долю секунды таких молекул станет тринадцать, затем — сорок, сто двадцать одна и так далее. На каждом шаге число молекул, изменивших траектории, примерно утраивается, так что уже через 50 столкновений их число сравняется с числом всех молекулы во фляге. Более реалистический расчет, учитывающий стол­к­новения молекул с измененными траекториями между собой, все равно показывает, что возмущение от удаленной молекулы распространяется со скоростью звука и охватит всю флягу за тысячную долю секунды.

Если мы даже не удалим молекулу, а лишь чуть-чуть ошибемся при измерении ее положения или скорости, то расчетные траектории все равно практически мгновенно перестанут совпадать с реальными. Математик Э. Борель подсчитал, что ошибка величиной 10^-100 в определении начальных положений или скоростей молекул одного моля спустя секунду приведет к тому, что их траектории не будут иметь ничего общего с расчетными. Но возмущение столь ничтожной величины вызывается перемещением 1 г вещества на 1 см на звезде Сириус (9 световых лет от Земли)! Так можно ли и после этого утверждать, что существует, хотя бы в принципе, возможность точно и однозначно выяснить судьбу каждой молекулы? Очевидно, нет.

С другой стороны, температура и давление газа не чувствительны к удалению молекулы или к слабому изменению начальных условий. Но эти величины пропорциональны средним значениям энергии и импульса молекул, вычисляемым с помощью теории вероятностей. Таким образом,

молекулярно-кинетическая теория впервые показала несостоятельность механического детерминизма и плодотворность статистического, вероятностного подхода в отношении многочастичных систем.

В молекулярно-кинетической теории появился совершенно новый подход к описанию состояния системы. Состояние описывалось теперь не значениями физических величин, а вероятностями этих значений. Этот подход оказался чрезвычайно плодотворным при построении фундаментальных естественнонаучных теорий XX века.