Уравнение неразрывности

Выведем вначале уравнение неразрывности массы вещества при его одномерном прямолинейном движении в пласте. Масса 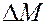вещества плотностью 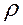в элементе пласта (рис. 27) длиной 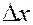, толщиной 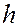и шириной 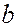, измеряемой в направлении, перпендикулярном к плоскости при пористости пласта 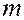, составит

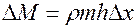(3.11)

Рис. 27. Схема элементарного объема прямолинейного пласта

Рис. 28. Схема элементарного пласта в трехмерном случае

Если считать, что в элемент пласта через его левую грань поступает вещество с массовой скоростью 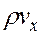, вытесняется из элемента с массовой скоростью и 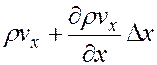, а накопленный объем его 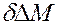за время 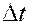, получим с учетом того, что в элемент вошло больше вещества, чем из него вышло:

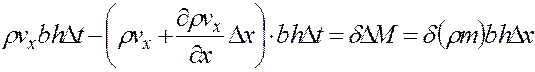. (3.12)

Из (3.12) имеем

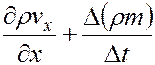(3.13)

при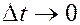

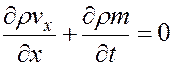(3.14)

Уравнение (3.14) и есть уравнение неразрывности массы вещества в пласте при одномерном прямолинейном движении насыщающего его вещества. Чтобы получить такое уравнение для трехмерного случая, необходимо рассмотреть баланс массы в объемном элементе пласта 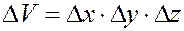(рис. 28). Рассматривая массовые скорости поступления вещества в куб и вытеснения из него, а также накопленный объем его в кубе, получим

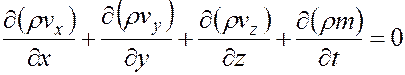. (3.15)

Уравнение (3.15) можно записать также в следующем общем виде:

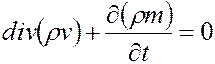. (3.16)

Уравнения (3.15), (3.16) — уравнения неразрывности массы вещества во время его движения при трехмерном измерении. Если в пласте одновременно движутся несколько веществ, находящихся как в газовой, так и в жидкой фазе, составляют уравнения неразрывности массы каждого вещества (компонента) в соответствующих фазах.