Метод симметрии
Теорема. Если однородное тело имеет плоскость, ось или центр симметрии, то центр тяжести его лежит на плоскости, оси или в центре симметрии.
На основании этой теоремы можно легко определить положение центров тяжести следующих тел:
1)Центр тяжести отрезка прямой лежит в его середине.
2)Центр тяжести окружности, круга, поверхности и объема шара находится в их геометрических центрах.
3)Центр тяжести периметра и площади параллелограмма, ромба, прямоугольника и квадрата лежит в точке пересечения их диагоналей.
4)Центра тяжести периметра и площади правильного многоугольника находится в центра вписанного (или описанного) круга.
2.Метод разбиения.
Этот метод применяется в случае, если данное тело можно разбить на конечное число частей, для которых положение центра тяжести заранее известно. Например, тело, показанное на рис.8.3.

Рис.8.3.
Тогда производят это разбиение и координаты центра тяжести всего тела определяют по указанным ранее формулам (8.4), (8.5) или (8.6). При этом число слагаемых в каждом из числителей будет равно числу частей, на которое разбито тело.
Замечание. Если тело имеет вырезы, то объемы или площади вырезов в указанных формулах берутся отрицательными.
3.Метод интегрирования.
Если тело нельзя разбить на конечное число частей, то применяется метод интегрирования (рис.8.4).

Рис.8.4.
Суть его в следующем: тело разбивают на произвольно малые объемы DVk, для которых указанные формулы принимают вид
xC= 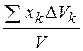 и т.д.
и т.д.
где xk, yk, zk -координаты некоторой точки, лежащей внутри объема DVk. Затем в этих равенствах переходят к пределу при DVk®0. Тогда стоящие в числителях суммы преобразуются в интегралы, распространенные на весь объем тела и формулы принимают вид:
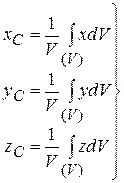 (8.7)
(8.7)
Аналогично получаются формулы для координат центра масс плоских фигур и линий
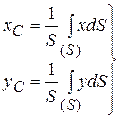 (8.8)
(8.8)
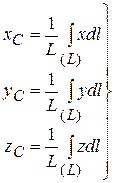 (8.9)
(8.9)
Дата добавления: 2015-02-25; просмотров: 1000;
