Уравнение движения электропривода. Определение времени пуска и торможения.
Уравнение движения электропривода имеет следующий вид:
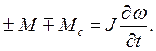 (5.1)
(5.1)
Из этого уравнения следует, что момент М, развиваемый двигателем, уравновешивается моментом сопротивления рабочей машины Мс и инерционным моментом. Инерционный момент проявляется только во время переходных режимов, когда изменяется величина угловой скорости привода. При ускорении привода этот момент направлен против движения, а при торможении он поддерживает движение.
Выбор знаков перед значениями моментов в формуле (5.1) зависит от режима работы двигателя и характера моментов сопротивления.
Уравнение движения электропривода позволяет определить зависимость моментов и угловой скорости от времени в течении переходного процесса.
Так как аналитическое решение уравнения движения электропривода затруднено вследствие нелинейности зависимостей Мдв = f(w) и Мс = f(w), оно может быть решено следующим образом.
Строятся механические характеристики электродвигателя Мдв = f1(w) и рабочей машины Мс = f2(w), графически находится их разность - кривая избыточного момента: Мизб = Мдв - Мс = f3 (w). Эта кривая заменяется ступенчатой кривой с участками, на которых избыточный момент постоянен и равен его средней величине Мизбi.
Далее определяется продолжительность разгона на каждом отдельном участке скоростей вращения, на которых избыточный момент является постоянным. Продолжительность разгона может быть определена двумя методами: графическим и графоаналитическим (ввиду сложности чисто аналитический метод не используется).
При решении задачи графоаналитическим методом время разгона на каждом отдельном участке определяется по следующему соотношению:
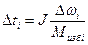 (5.2)
(5.2)
где J - момент инерции системы, кг*м2;
Dwi - интервал скорости вращения на i - м участке, с-1;
Мизбi - средний избыточный момент на i-м участке, Н*м.
Тогда полная продолжительность пуска будет равна сумме продолжительностей разгона на отдельных участках:
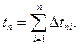 (5.3)
(5.3)
Пример 5
Определить продолжительность торможения и разгона электропривода вентилятора. Данные двигателя: тип 4А80В2УЗ, Рн = 2,2 кВт; cosjн= 0,87;hн = 0,83;mп = 2,1; mм = 1,4;mк = 2,6; Sкр= 38%; Sн = 4,3%; Jдв= 0,0021 кг*м2; Jрм = 0,006 кг*м2; Мнс = Мнд ; рабочая машина находится непосредственно на валу электродвигателя.
Решение
Рассчитаем механическую характеристику двигателя.
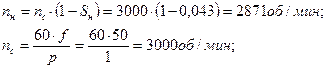
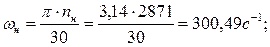
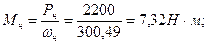
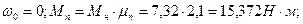
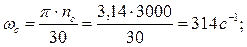
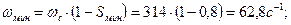
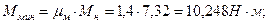
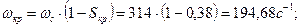
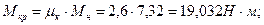
Дополнительно для более точного построения механической характеристики рассчитаем значения моментов при S = 0,15 и S = 0,5. Результаты расчетов сводим в таблицу 5.1.
Расчет ведем по общей формуле:
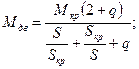
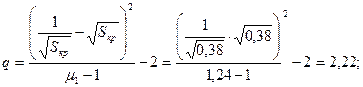
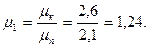
Таблица 5.1 – Результаты расчетов механической характеристики двигателя и
рабочей машины
| S | 0,043 | 0,15 | 0,38 | 0,5 | 0,8 | 1,0 | |
| w, с-1 | 300,5 | 266,9 | 194,7 | 62,8 | |||
| Мдв , Н* м | 7,32 | 15,6 | 19,03 | 18,69 | 10,25 | 15,37 | |
| Мс , Н*м | 7,79 | 7,32 | 6,24 | 4,34 | 3,59 | 2,42 | 2,2 |
| Мизб , Н*м | -7,79 | 9,36 | 14,7 | 15,1 | 7,83 | 13,17 |
Рассчитаем механическую характеристику рабочей машины. Механическая характеристика рабочей машины описывается следующим уравнением:
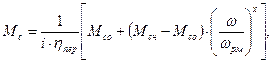 (5.4)
(5.4)
где Мсо - начальный момент сопротивления рабочей машины, Н*м,
Мсо = 0,З*Мсн;
Мсн - момент сопротивления при номинальной угловой скорости, Н*м;
Мсн = Мнд - по условию;
i - передаточное отношение;
hпер - КПД передачи;
wрм - номинальная угловая скорость рабочей машины, с-1;
х - показатель степени, характеризующий изменение момента сопротивления с изменением угловой скорости. Для вентиляторов х =2.
Результаты расчета механической характеристики рабочей машины сведены в таблицу 5.1.
По полученным данным строим на одном графике зависимости:
Мдв = f1(w); Мс = f2(w);Мизб = f3(w); (см - рисунок 5.1).
Сведем расчеты по определению времени пуска в таблицу 5.2. Приведенный момент инерции системы может быть определен по следующему соотношению
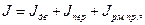 (5.5)
(5.5)
где Jдв - момент инерции двигателя, кг*м2;
J пер - момент инерции передачи, кг*м2;
Jрм.пр. - приведенный к валу двигателя момент инерции рабочей машины,кг*м2.
Момент инерции рабочей машины приводится к валу двигателя следующим образом:
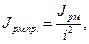 (5.6)
(5.6)
где i - передаточное отношение от вала электродвигателя к рабочей машине.
Если рабочая машина совершает поступательное движение, приведенный момент инерции определяется по соотношению
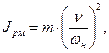 (5.7)
(5.7)
где т - масса поступательно движущихся частей, кг;
ν - линейная скорость поступательно движущихся частей, м/с;
wн - номинальная угловая скорость вращения вала двигателя, с-1.
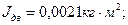
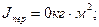
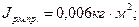
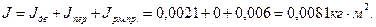
Таблица 5.2 – Результаты расчетов времени пуска
| Участок | |||||||
| wнач , с-1 | |||||||
| wкон , с-1 | |||||||
| Dw, с-1 | |||||||
| Мизб.i , Н*м | 10,5 | 7,5 | 11,5 | ||||
| Dtпi , с | 0,038 | 0,054 | 0,035 | 0,027 | 0,014 | 0,037 | 0,0405 |
| tп=SDti ,с | 0,2455 |
Аналогичным образом определяется продолжительность торможения. Так как для торможения не используется никаких дополнительных средств, то остановка привода происходит исключительно за счет момента сопротивления. Поэтому для определения времени торможения необходимо кривую Мс = f2(w) заменить ступенчатой с участками, на которых Мс = const . Тогда продолжительность торможения на каждом отдельном участке угловых скоростей будет равна:
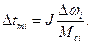 (5.8)
(5.8)
Полная продолжительность торможения будет равна
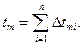 (1.29)
(1.29)
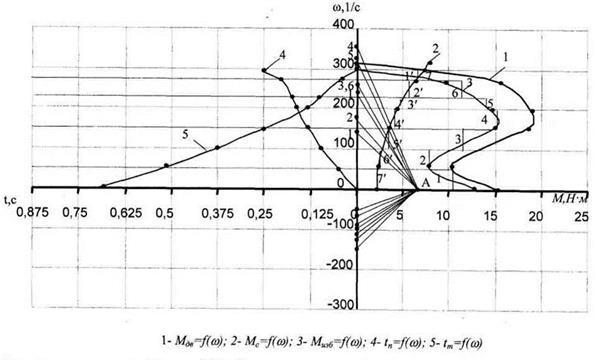
Рисунок 5.1 – К определению времени пуска и времени торможения.
Сведем расчеты по определению продолжительности торможения в таблицу 5.3.
Таблица 5.3 - Результаты расчетов времени торможения
| Участок | 1’ | 2’ | 3’ | 4’ | 5’ | 6’ | 7’ |
| wнач , с-1 | |||||||
| wкон , с-1 | |||||||
| Dw, с-1 | |||||||
| Мс.i , Н*м | 4,6 | 3,8 | 2,7 | 2,5 | |||
| Dtтi , с | 0,029 | 0,0675 | 0,044 | 0,1 | 0,135 | 0,15 | 0,162 |
| tт=SDtтi,с | 0,6875 |
Дата добавления: 2015-02-25; просмотров: 5987;
