Определение длины отрезка и углов наклона его к плоскостям проекций

Угол наклона прямой к плоскости проекций определяется как угол, составленный прямой с ее проекцией на эту плоскость.

На рис. 39 показан отрезок АВ и его горизонтальная проекция А₁В₁. Проведя прямую ВК ‖ А₁В₁, получим прямоугольный треугольник АВК. Длина отрезка АВ равна гипотенузе этого треугольника, прилежащий катет КВ равен горизонтальной проекции отрезка, т.е. КВ = А₁В₁, противолежащий катет равен разности координат Z точек Аи В (∆ Z = Z_А – Z_В).

На рис. 40 определен угол между отрезком прямой АВ и плоскостью проекций П₁.

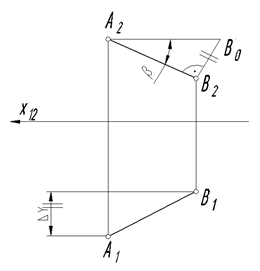
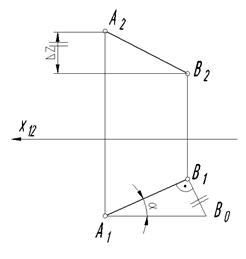Угол между горизонтальной проекцией А₁В₁ и натуральной величиной А₁В₀ является искомым углом α. Данный метод определения натуральной величины прямой называют еще методом прямоугольного треугольника.

Рис. 40 Рис. 41

Контрольные задания по теме «Прямая"

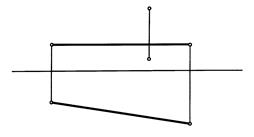
1. Через точку Е провести прямую, параллельную плоскости П₁, под углом 15⁰ к плоскости П₂.

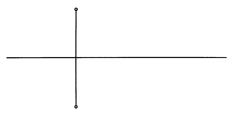
2. Построить следы прямой и указать, через какие четверти пространства она проходит.

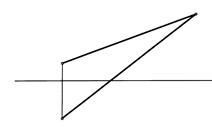
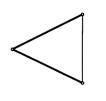
3. Определить угол наклона отрезка прямой АВ к плоскости проекций П_2.

5. Отрезок АВ разделить точкой С внутренним делением в отношении АС : СВ = 1:4.

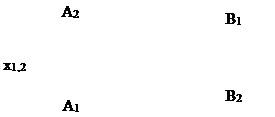
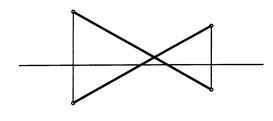
Пример 1.Провести через точку Е прямую, пересекающую прямую АВ и параллельную горизонтальной плоскости проекций.

Проведем через Е₂проекцию h (h₂ ‖ х, т.к. Z = const). Прямые пересекаются, если имеют общую точку.

1₂ = А₂В₂ Ⴖ h₂ ; 1₁ Î А₁В₁.

Затем через Е₁ и 1₁ проводим h₁.

Пример 2.Определить натуральную величину отрезка АВ.

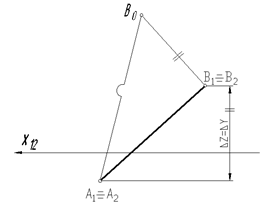
Для определения натуральной величины отрезка АВ воспользуемся методом прямоугольного треугольника. Прилежащим катетом будет являться горизонтальная проекция А₁В₁ (или фронтальная – А₂В₂), противолежащим катетом – разность координат Z (или Y) точек А и В. Гипотенуза будет равна натуральной величи-

Рис. 42 не прямой АВ.

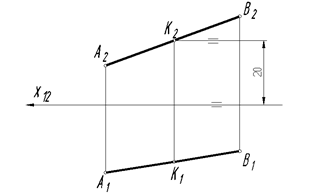
Пример 3.На прямой АВ найти точку К, если удаление ее от плоскости проекций П₁ равно 20 мм. Удаление точки К от П₁ определяется координатой Z (Z=20). Откладываем это значение по направлению координатной оси Z и проводим вспомогательную прямую параллельную оси X. Получили фронтальную проекцию К­₂ точки К; К₁ Î А₁В_1.

Контрольные вопросы.

1. Какую прямую называют прямой общего положения?
2. Перечислите прямые частного положения, дайте определение каждой из них и укажите особенности их проекций.
3. Как на чертеже разделить отрезок прямой линии в заданном отношении?
4. Как по чертежу определить взаимное расположение прямых в пространстве?
5. Какие точки называются конкурирующими?
6. В каком случае прямой угол проецируется на плоскость проекций без искажения?
7. Что называется следом прямой линии?
8. Как построить следы прямой линии на чертеже?
9. Какая координата равна нулю:

- для фронтального следа прямой;

- для горизонтального следа прямой?

10. Как найти натуральную величину отрезка прямой? Как определить углы наклона отрез-

ка прямой к плоскостям проекций П₁ и П₂?