Взаимное положение прямых
Две прямые в пространстве могут пересекаться, скрещиваться и быть параллельными.
1. Пересекающиеся прямые – прямые, имеющие одну общую точку.
|
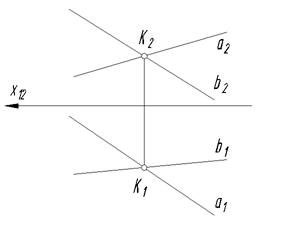
Если прямые пересекаются, то на эпюре пересекаются и их одноименные проекции, а проекции точки пересече 
ния К лежат на одной линии связи, т.е.
К = а Ⴖ b Þ а1 Ⴖ b1; К2 = а2 Ⴖ b2.
2. Параллельные прямые – прямые, пересекающиеся в несобственной точке (т.е. прямые, которые лежат в одной плоскости и пересекаются в бесконечно удаленной точке).
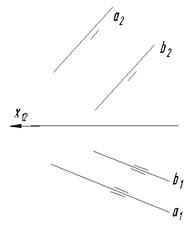
Если прямые параллельны, то параллельны и их одноименные проекции на все три плоскости проекций. Для того, чтобы сделать вывод о параллельности прямых общего положения, достаточно параллельности их одной проекций на две плоскости проекций, т.е.
а ‖ b Þ а1 ‖ b1; а2 ‖ b2.
Для прямых частного положения необходимо, чтобы были параллельны их проекции на той плоскости проекций, которой эти прямые параллельны.
3. Скрещивающие прямые – прямые, не имеющие ни одной общей точки.
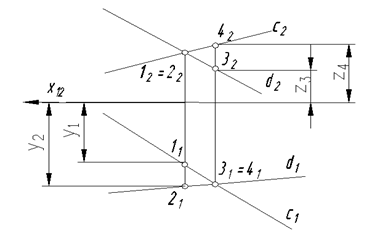На эпюре (рис. 34) точки пересечения проекций этих прямых не лежит на одной линии связи, перпендикулярной к оси Х. На чертеже скрещивающихся прямых c и d точки 1, 2 и 3, 4 называются конкурирующими.
На горизонтальной проекции будет видимой та из конкурирующих точек 3 и 4, которая расположена выше относительно П1 (Z4 >Z3), т.е. точка 4; на фронтальной проекции видимой будет точка 2, т.к. она расположена ближе к наблюдателю (Y2>Y1).
Дата добавления: 2015-02-25; просмотров: 1135;