Спекулятивный спрос на деньги.

Мы рассмотрели два мотива спроса на деньги: трансакционный спрос и спрос, вызванный предосторожностью. Оба эти мотива относятся к функции денег как средства обращения, поскольку в обоих случаях индивид держал деньги для того, чтобы оплатить необходимые расходы. Однако, как мы обсуждали ранее, деньги выполняют и ряд других функций, в частности, служат средством сохранения стоимости. Выполняя эту функцию, деньги выступают не только в виде наличных средств, но и виде различного рода депозитов, например срочных вкладов. Таким образом, говоря о спекулятивном спросе на деньги, мы объясняем поведение агрегата М2, в то время как трансакционнный спрос и спрос из предосторожности относятся скорее к М1.

Итак, рассмотрим, какими критериями руководствуется индивидуум, когда использует деньги как средство сохранения стоимости. На первый взгляд, использование денег для сохранения и приумножения своего богатства кажется не вполне продуманным решением. Действительно, деньги по сравнению с другими финансовыми активами (например, акциями или облигациями) приносят значительно меньший доход, так не разумнее ли все свои средства вкладывать в более доходные активы? Проблема состоит в том, что активы с большей доходностью связаны и с большим риском: доходность является случайной величиной и для более высокодоходных активов наблюдается больший разброс доходностей, то есть больший риск. Если индивид не склонен к риску, то он предпочитает диверсифицировать свои вложения и в результате часть богатства хранит в виде наименее рискованного актива, то есть в виде денег.

Рассмотрим простейшую модель выбора оптимального портфеля ценных бумаг. Условно разделим все финансовые активы на две группы. К первой группе отнесем безрисковые активы. Такие активы обладают очень низкой ожидаемой доходностью. Эту группу активов мы и будем называть деньгами. Обозначив ожидаемую доходность через 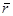, а риск (который измеряется как корень из дисперсии, то есть, среднеквадратическое отклонение) через s мы можем дать характеристику первого актива (денег): 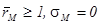. Второй актив, который будем условно называть альтернативным активом, характеризуется большей доходностью и большим риском: 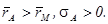Обозначим через a (0£a£1) долю вложений в безрисковый актив (деньги), тогда доля вложений в рисковый (альтернативный) актив будет равна (1-a). Если W- богатство индивид, то вложения в безрисковый актив будут равны aW.

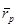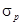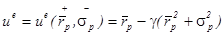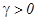Будем считать, что индивидуум не склонен к риску: чем выше риск (при прочих равных), тем ниже уровень ожидаемой полезности. Будем полагать, что ожидаемая полезность зависит от ожидаемой доходности портфеля положительно и от риска портфеля , который мы измеряем с помощью среднеквадратического отклонения, - отрицательно: , где [14]. Мы можем изобразить линии уровня этой функции в пространстве риск -ожидаемая доходность. Эти линии представляют из себя окружности: 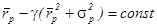с центром в точке 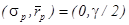, как изображено на рисунке 3.

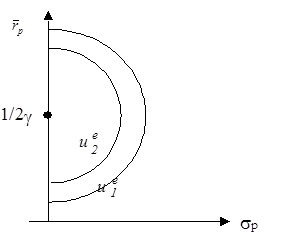
Рисунок 3. Кривые безразличия в модели Марковица

Далее будем считать, что все рассматриваемые активы имеют ожидаемые доходности, лежащие ниже точки насыщения: .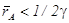

Теперь определим множество, на котором индивидуум осуществляет свой выбор. Для этого выразим ожидаемую доходность и риск каждого портфеля через доходности и риски составляющих его активов. Обозначим через x_i случайную величину, соответствующую валовой доходности актива i, где i={М, А}. Поскольку доля вложений в безрисковый актив равна a, а в рисковый – (1-a), то ожидаемая валовая доходность портфеля равна:

.

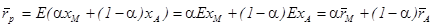Итак, ожидаемая доходность портфеля равна средневзвешенной величине ожидаемых доходностей входящих в портфель активов.

Теперь определим риск портфеля, который равен квадратному корню из дисперсии (обозначим дисперсию через Var). Итак, дисперсия портфеля может быть выражена через дисперсии входящих в портфель активов следующим образом:

(7) .

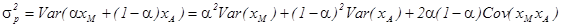В нашем случае ковариация рассматриваемых активов равна нулю, поскольку один из активов является безрисковым активом. Учитывая, что 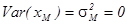, 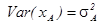и 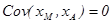, соотношение (7) примет вид: .

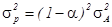Таким образом, мы получили, что ожидаемая доходность и риск портфеля равны:

(8) .

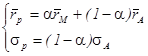Преобразуя систему (8) получаем:

(9) .

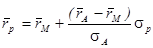Множество портфелей, удовлетворяющих условию (9) – это прямая, выходящая из точки 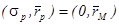под углом 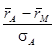. Учитывая, что a лежит между нулем и единицей, мы получаем отрезок [AB], соответствующий границе допустимого множества портфелей (смотри рисунок 4).

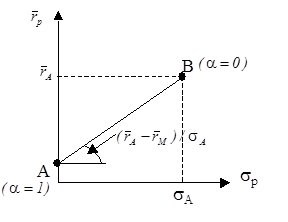
Рис. 4. Множество допустимых портфелей, состоящих из комбинации безрискового актива с нулевой ожидаемой доходностью и рискового актива.

Наложив на этот же график кривые безразличия, мы можем проиллюстрировать выбор оптимального портфеля (смотри рисунок 5). Итак, оптимум достигается в точке касания кривой безразличия с границей множества допустимых портфелей. Как мы видим, в оптимальной точке a строго больше нуля, но меньше единицы. Это означает, что потребитель выбирает стратегию диверсификации, то есть старается сократить риск путем вложений в разные активы, в том числе в безрисковый актив (то есть, деньги).

Рисунок 5. Выбор оптимального портфеля

Какие же факторы влияют на наше решение об оптимальном распределении богатства между различными активами и, в частности, о вложениях в безрисковый актив, то есть, в деньги. Во-первых, это ожидаемая доходность и риск альтернативных активов. И, наконец, сама величина богатства также влияет на сумму вложений в каждый из активов. Проиллюстрируем роль этих параметров, решив задачу выбора оптимального портфеля:

.

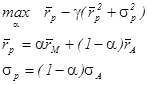Из условия первого порядка находим оптимальную долю вложений в безрисковый актив: .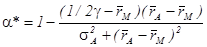

Из полученной формулы следует, что с увеличением риска по альтернативному активу (с ростом 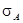) спрос на безрисковый актив будет расти. Нужно упомянуть еще один фактор, влияющий на величину спроса на безрисковый актив. Поскольку абсолютная величина спроса на деньги равна aW, то величина реального богатства также имеет значение. Чем больше реальное богатство, тем выше спрос на деньги. Увеличение доходности безрискового актива и/или падение доходности альтернативного актива также приведет к росту спроса на безрисковый актив (деньги) при определенном соотношении параметров задачи (в данном случае, если наклон границы множества допустимых портфелей меньше единицы).

Таким образом, спрос на безрисковый актив будет тем больше, чем выше собственная ожидаемая доходность денег, чем ниже ожидаемая доходность и выше риск альтернативного актива. Итак, мы можем просуммировать все факторы, влияющие на спекулятивный спрос на деньги с помощью следующей функции спекулятивного денежного спроса: 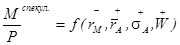, где 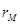- собственная доходность денег, 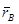- ожидаемая доходность альтернативного актива, 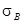- риск по альтернативному активу, W-реальное богатство.