Билет 5
1. 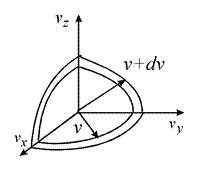 Тепер нас не цікавлять напрямки швидкостей. Будемо шукати імовірність того, що абсолютне значення швидкості знаходиться у межах
Тепер нас не цікавлять напрямки швидкостей. Будемо шукати імовірність того, що абсолютне значення швидкості знаходиться у межах 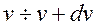 .
.
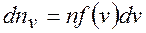
У просторі швидкостей проведемо дві сфери радіусами 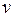 та
та 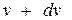 . Кількість молекул, що попадає у проміжок між сферами,
. Кількість молекул, що попадає у проміжок між сферами,
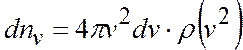 .
.
Скористаємось отриманим раніше виразом для густини швидкостей
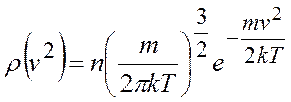 і підставимо його у рівняння
і підставимо його у рівняння
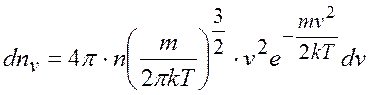 . Порівнявши це рівняння із
. Порівнявши це рівняння із
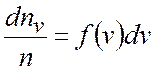 , отримаємо
, отримаємо
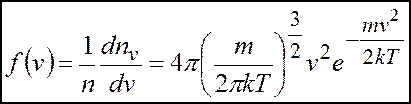 .
.
Це – функція розподілу молекул за абсолютними швидкостями, отримана Максвеллом. Вона визначає, як ми вже зазначали, частку молекул, швидкості яких попадають в одиничний інтервал швидкостей в околі значення швидкості 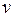 .
.
А тепер давайте повернемось до того значення 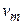 , яке ми пропустили. Подивимось на графік залежності
, яке ми пропустили. Подивимось на графік залежності 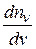 від
від 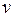 . На ній при значенні
. На ній при значенні 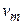 є максимум. Що це означає ? Що таку швидкість має найбільша кількість молекул, тобто імовірність того, що швидкість молекули близька до
є максимум. Що це означає ? Що таку швидкість має найбільша кількість молекул, тобто імовірність того, що швидкість молекули близька до 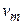 є найбільшою. Ця швидкість отримала назву найімовірнішої швидкості. Знайти її значення можна з рівності нулю похідної функції розподілу
є найбільшою. Ця швидкість отримала назву найімовірнішої швидкості. Знайти її значення можна з рівності нулю похідної функції розподілу 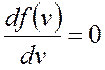
Відкинувши константи, маємо 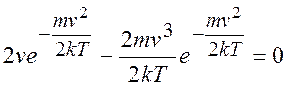 ;
; 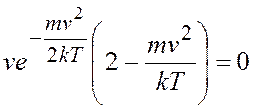 ;
; 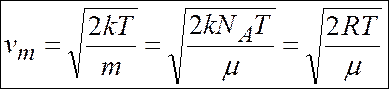 ..
..
Дата добавления: 2015-01-13; просмотров: 1008;
