Расчет валов на виброустойчивость

Быстроходные валы рассчитывают не только на прочность и жесткость, но и на виброустойчивость, так как во время работы пе­редач в валах возникают колебания:

· поперечные (изгибные),

· угловые (крутиль­ные) и

· продольные (растяжения – сжатия).

Для большинства быстроходных валов наиболее опасны изгибные колебания, кото­рые вызываются неуравновешенностью насаженных на валы деталей, погрешностью их изготовления и монтажа. Связанные с этим инерционные си­лы являются возмущающими и вызывают вынуж­денные поперечные колебания валов.

Если частота возмущающих сил совпадает с частотой собственных колебаний вала или кратна ей, то наступает явление резонанса, т.е. амплитуда колебаний вала резко возраста­ет. Это может привести к разрушению вала и его опор.

Вспомним, что собственными (свободными) колебаниями называют колебания, которые могут возбуждаться в системе под действием начального толчка. Форма и частота свободных колебаний определя­ются массой и упругостью системы.

Резонанс очень опасен для прочности валов, их опор и машины в целом, поэтому его следует избегать. Наиболее часто резонанс предотвращают за счет изменения частоты собственных колебаний конструкции, гораздо реже – за счет изменения частоты внешней на­грузки [2, с.262].

Вал, рассматриваемый в расчетах как балка переменного сечения, несущая сосредоточенные нагрузки, имеет, вообще говоря, бес­конечное число степеней свободыи соответствующее число частот собственных колебаний. Однако определяющее практическое значение имеет первая наинизшая частота собственных колебаний вала (наибо­лее опасная для его прочности) называемая основной.

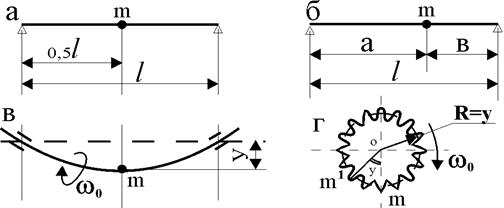Рис. 1.6. Схемы валов с сосредоточенной массой m:

а – равноудалённая масса m относительно опор;

б – разноудалённая масса m относительно опор вала

Если невесомый вал с сосредоточенной массой m(рис.1.6, а, б) вывести из состояния равновесия, то он будет колебаться относительно геометрической оси вращения с поперечной секундной частотой собственных колебаний (ЧСК), с ^{– 1} [2, с.334]:

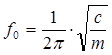
(1.15)

где С – изгибная жесткость вала, С = 48Е×J / l ³ (см. рис.1.6, а),

C = 3E×J× l / (a × b)² (см. рис. 1.6, б).

Еслизатем заставить этот вал вращаться вокруг его геометричес­кой оси, то за время одного полного оборота вала (за 2p рад) центр тяжести колеблющейся массы m совершит уже другое число колебаний [7, с. 595]:

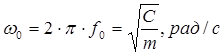(1.16)

При этом за 1с центр тяжести массы mпройдет по окружности радиуса R = удугу mm^/,которой соответствует центральный угол j(см. рис.1.6, г).

Величинаw₀называется основной круго­вой частотой собственных колебаний вала. Как видно из ф. (1.16), основная круговая ЧСК определяется только изгибной жесткостью ва­ла Си массой груза mдля невесомых валов (т.е. для валов, чья масса много меньше массы груза и в расчетах не учитывается).

Основную круговую ЧСК вала с учетом его собственной массы наиболее просто вычислить, если к массе груза прибавить приведенную массу вала. Так, например, для двухопорного вала с грузом посередине (см. рис. 1.6, а) при поперечных колебаниях коэффициент приведения равен 17/35 [1, с.333].

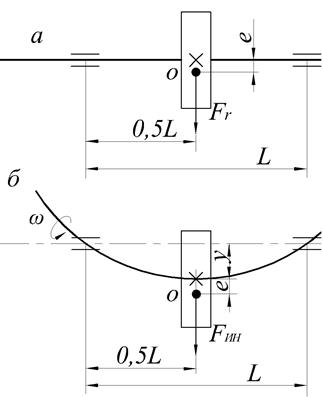
Рис. 1.7. Расчетная схема двух­опорного вала с диском

Быстро вращающиеся валы с насаженными на них деталя­ми должны быть сбалансированы.В действительности всегда есть несовпадение центра тяжести такого вала с его геометри­ческой осью вращения на не­которую величину “е”, назы­ваемую эксцентриситетом (рис. 1.7, а).

При вращении вала с уг­ловой скоростью wпояв­ляется центробежная силаF_ИН от несбалансированной массы диска, вызывающая про­гиб вала “у”. При этом центр тяжести диска, т. О, будет вращаться по ок­ружности радиуса R = y+e.

F_ИН = F_У или m×w²×(y + e)= с×y(1.17)

Разрешив равенство (1.17) относительно прогиба вала, получим:

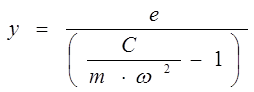(1.18)

В знаменателе ф. (1.18) отношение “С/m”представляет собой квадрат основной круговой ЧСК вала. Следовательно, ф. (1.18) можно записать иначе:

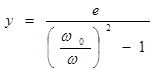(1.19)

Из ф. (1.19) следует, что с увеличением угловой скорости вращения вала (но при w < w₀ ) прогиб вала возрастает (рис. 1.8) и при

w = w₀ прогиб вала становится (теоретически) бес­конечным, т.е. наступает ре­зонанс.

Именно поэтому угловую скорость вращения вала, равную основной круговой ЧСК, называют критической и обозначают w_кр.

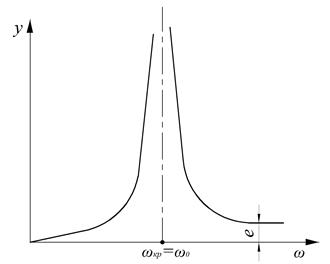
Рис. 1.8. Зависимость прогиба вала от угловой

скорости вращения

В действительности же из-за трения и конструктивных ограничений в опорах прогиб вала имеет конечную величину. Однако, работа в режиме резонанса опасна из-за перегрузки материала вала и его опор. По соображениям безопасности экс­плуатации машины стремятся применять жесткие валы, для которых рабочий диапазон угловых скоростей: w < 0,7w_кр [2. с.265].

При дальнейшем увеличении угловой скорости вращения вала (при w >w_кр) центр тяжести диска само устанавливается между геометрической осью вращения вала и его изогнутой осью (рис. 1.9).

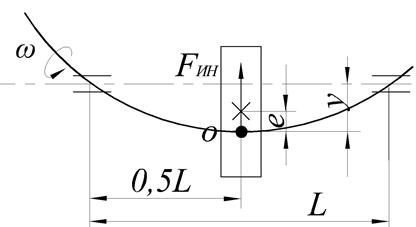
Рис. 1.9. Расчетная схема двухопорного вала,

работа­ющего при n>n_крит

Прогиб вала в этом случае вычисляют по зависимости [7, с.612]:

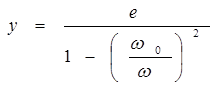(1.20)

Как видно из ф. (1.20), после прохождения через критическую ча­стоту вращения (при w >w₀) прогиб вала уменьшается и при­ближается по величине к эксцентриситету.

При значительных угловых скоростях наступает дина­мическое центрирование вала, т.е. центр тяжести диска достигает геометричес­кой оси вращения: у = е (см. рис. 1.9). На практике при больших “w”, например: в цент­рифугах, применяют валы, рабо­тающие в зарезонансной зоне (при w >1,3w _кр). Для того, чтобы отойти от области резо­нанса, валы делают повышенной податливости[1, с.335].

Итак, резонанс – это опасное для прочностилюбого вала яв­ление и наблюдается при сов­падении угловой скорости вра­щения вала и основной круго­вой ЧСК вала, т.е. при w =w₀ = w_кр.

Соответствующее критическое число оборотов в минуту определяют по зави­симости:

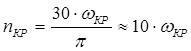(1.21)

Если вычислить w_КРчерез статический прогиб вала у_ст(в сантиметрах), то ф. (1.21) примет вид:

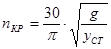, об/мин, (1.22)

где g – ускорение свободного падения; g= 981см/с².