Временные параметры вероятностных сетей

На практике встречаются проекты, которые характеризуются тем, что время выполнения отдельной операции или работы, равно как и время, идущее на осуществление всего проекта, представляют собой случайные величины. В этом случае наиболее важными временными параметрами вероятностных сетей являются параметры законов распределения сроков наступления всех событий сети; срок наступления завершающего события при этом совпадает с продолжительностью всего проекта.

Для определения параметров вероятностных сетей можно использовать аналитические методы, статистическое моделирование и методы усреднения.

Рассмотрим метод усреднения, который широко применяется при анализа вероятностных сетей. Суть этого метода состоит в использования для вычисления вероятностных характеристик сети оценок математического ожидания и дисперсии работ.

Исходными данными для метода усреднения являются вероятностные оценки продолжительности каждой работы.

Для того чтобы использовать метод PERT, для каждой работы, время выполнения которой является случайной величиной, необ­ходимо определить три временные оценки продолжительности работ:

1. Оптимистическая 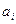— это минимальное время ( 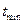), в течение которого может быть выполнена данная работа в предположении наиболее благоприятного стечения обстоятельств;

2. Наиболее вероятная (нормальное) 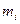оценка продолжительности ( 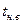)— это время выполнения данной работы при наиболее часто встречающихся условиях выполнения работ;

3. Пессимистическая 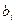— это максимальное возможное время ( 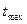) выполнения данной работы в предположении наиболее неблагоприятного стечения условиях.

Учитывая, что время выполнения работы хорошо описывается бета-распределением, среднее или ожидаемое время 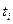выполне­ния работы i может быть оценено по формуле

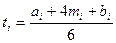.(5.10.1)

Если время выполнения работы i известно точно и равно 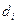, то = = = = .

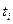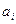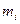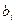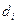Располагая указанными тремя оценками времени выполнения работы, можно рассчитать общепринятую статистическую меру неопределенности — дисперсию 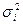или вариацию 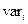времени выполнения работы i:

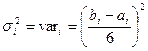. (5.10.2)

Если время выполнения работы i известно точно, то 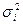= = 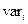0.

Пусть Т — время, необходимое для выполнения проекта. Если в проекте есть работы с неопределенным временем выполнения, то время T является случайной величиной.

Предполагается, что в интервале между оптимистической ( 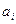) и пессимистической ( 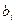) оценками заключены все возможные продолжительности операции (работы). Наиболее вероятная оценка m не обязательно совпадает со средней точкой отрезка 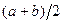и может лежать справа и слева от нее. Благодаря таким свойствам интуитивно определяется предположение, что продолжительность каждой работы подчиняется бета-распределению с модой в точке m и концами в точке a и b. На рис. 5.13 показаны три случая бета-распределению: симметричное, асимметричное вправо, асимметричное влево.

Рис.5.13.Три случая бета-распределению

Выражения для математического ожидания Тоже и дисперсии 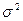бета-распределению выводится следующим образом. Предполагается, что вес средней точки 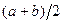) вдвое меньше веса наиболее вероятной m. Таким образом, величина Тоже представляет собой арифметическое среднее величин 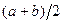) и 2m, т.е.

.

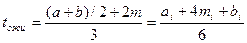Размах(a,b) применяется равным около шести средных квадратичных отклонений распределения, так как – 90% или более любой плоскости вероятности лежит в пределах трех средных квадратичных отклонений от математического ожидания. Таким образом,

.

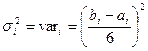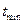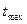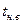Значения параметров , и определяются исполнителем работ или соответствующим экспортом. Выбор этих значений зависит от ряда обстоятельств, некоторые из них подчас не поддаются анализу. В итоге эти величины выступают как случайные.

Ряд основных параметров вероятностных сетей - ранние и поздние сроки наступления событий и выполнения работ, резервы времени событий и работ – определяются так же, как соответствующие параметры детерминированных сетей. Необходимо лишь помнить, что в этом случае параметры являются некоторыми усредненными величинами.

Дополнительно к параметрам, определяемым для детерминированных сетей, при анализе вероятностных сетей вычисляют также оценки дисперсии сроков наступления событий, служащие мерой их возможного разброса, а также вероятности наступления события в плановые (директивные) сроки.

Оценки дисперсии 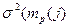равного срока наступления события 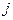применяется равной сумма оценок дисперсии работ наибольшего по продолжительности пути, предшествующую событию 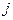и определенного по ожидаемых значениям продолжительноси работ.

Если таких путей несколько, то оценка дисперсии равна максимальному значению из оценок дисперсией этих путей.

В качестве приближенного закона распределения срока наступления завершающего события принимается нормальное распределение со значением Тоже и дисперсией 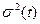срока наступления этого события. В соответствии с этим вероятность 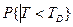того, что продолжительность выполнения проекта не перевисит заданного срока 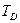вычисляется по формуле:

,

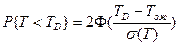где значение 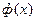берется из таблицы нормального распределения.

Сетевое планирование в условиях неопределенности

Чаще всего продолжительность выполнения работы сетевого графика является неопределенной, в математическом понимании – случайной величиной. Если известен закон распределения случайной величины, то нетрудно найти две ее важнейшие характеристики: среднее значение (МОЖ) и дисперсию. Очевидно, как правило, для сетевого планирования уверенно судить о законе распределения не удается: Поэтому выработана следующая методика.

Рассмотрим сетевой график следующем виде (рис.5.14).

Рис.14.

Временные характеристики сетевого графика даны в таблице 2

Таблица 5.2

Работы(i-j)	Оценки времени выполнения	Дисперсия средного времени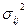
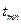
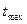
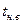
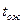
(1,2)					1,78
(1,3)
(1,4)					7,11
(2,5)
(3,7)					2,78
(4,6)					2,78
(5,6)		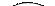			1,78
(6,7)		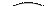			1,78

Получим, что Ткр =29 (1-2-5-6-7), а его дисперсия .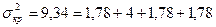

Процесс определение резервов времени работ не отличается от соответствующего расчета в детерминированном случае. Их значения смотри в таблице раздела “Резервы времени” (мы рассматриваем часть сетевого графика от основного, ограничившись семью

событиями, где заменены на ). ).

В качестве приближенного закона распределения срока наступления завершающего события применяется нормальное распределение со значением Ткр =Тож и дисперсия 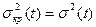срока выполнения этого события. В соответствии с этим вероятность 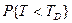того, что продолжительность выполнения проекта не превысит заданного срока 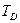, вычисляется по формуле

.

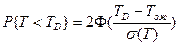Для нашего случая Ткр =Тож=29 с дисперсией .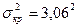

Тогда если установленный срок 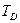=31, то вероятность выполнения комплекса работ за этот срок равна:

.

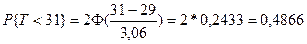Это означает, что имеется 48 шансов из 100, что работы будут завершены за 31 день или раньше.

Вероятность же выполнения комплекса работ за заданный срок, равный 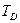=35 дням, будет:

.

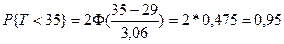Следует осторожно относиться к вычисленному среднему сроку завершения проекта Ткр =Тож, так как при большой дисперсии 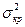вероятны весьма значительные отклонения от этого срока, ибо дисперсия срока наступления конечного события - это накопленная дисперсия всех работ критического пути, так что практических ее величина не может быть незначительной.