Пример 1. Реконструкция торгового центра.
Департамент Юго-Западного округа Москвы рассматривает возможность реконструкции торгового центра у станции метро «Юго-Западная». После сноса старых палаток проектом предусматривается строительство павильонов для сдачи их в аренду торговым фирмам. Работы, которые необходимо выполнить при реализации проекта, а также их взаимосвязь и время выполнения указаны в следующей таблице:
| Работа | Содержание работы | Опорные работы | Время выполнения, недели |
| A | Подготовить архитектурный проект | - | |
| B | Определить будущих арендаторов | - | |
| C | Подготовить проспект для арендаторов | A | |
| D | Выбрать подрядчика | A | |
| E | Подготовить документы для получения разрешения на строительство | A | |
| F | Получить разрешение на строительство | E | |
| G | Осуществить строительство | D, F | |
| H | Заключить контракты с арендаторов | B, C | |
| I | Вселить арендаторов в павилоны | G, H |
Вопросы:
1. Сколько работ на критическом пути?
2. Какова длина критического пути?
3. На сколько недель можно отложить начало выполнения работы Е, чтобы это не повлияло на срок выполнения проекта?
4. На сколько недель можно отложить начало выполнения работы В, чтобы это не повлияло на срок выполнения проекта (полный резерв времени)?
5. На сколько недель можно отложить начало выполнения работы С, чтобы это не изменило наиболее поздний срок наступления последующего события (свободный резерв времени)?
Решение. Для того чтобы определить срок выполнения проекта, достаточно найти длину критического пути. Для этого построим графическое представление проекта (рис. 5.10).
Рис.5.10. Сетевой модель для примера 1
Критический путь для этого проекта может быть найден с помощью прямых расчетов по методу СРМ.
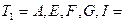 5+1+4+14+2=26 недели,
5+1+4+14+2=26 недели,
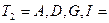 5+3+14+2=24 недели,
5+3+14+2=24 недели,
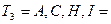 5+4+12+2=23 недели,
5+4+12+2=23 недели,
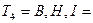 6+12+2=20 недели.
6+12+2=20 недели.
Наиболее короткий путь является путь 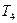 . Этот путь не содержит много работы проекта. Поэтому 20 недели недостаточно, чтобы выполнить все работы. Наиболее длинный путь является путь
. Этот путь не содержит много работы проекта. Поэтому 20 недели недостаточно, чтобы выполнить все работы. Наиболее длинный путь является путь 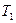 . В этот путь также не входит некоторые работы проекта, однако 26 недели достаточно, чтобы выполнить все работы комплекса, и этот путь называется критическим.
. В этот путь также не входит некоторые работы проекта, однако 26 недели достаточно, чтобы выполнить все работы комплекса, и этот путь называется критическим.
Рассчитаем временные параметры по этапам.
Этап 1.При вычисленни 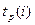 перемещаемся по сетевому графику от исходного события 1 к завершающему событию 7.
перемещаемся по сетевому графику от исходного события 1 к завершающему событию 7.
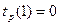 .
.
В событие 2 входит только одна работа
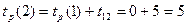 .
.
В событие 3 входит 2 работы: B и C
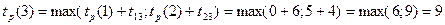 .
.
Аналогично
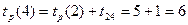 .
.
В событие 5 входит 2 работы: D и F
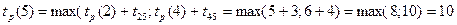 .
.
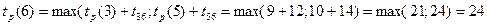 .
.
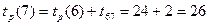 .
.
Таким образом, вычислили продолжительность критического пути, который равен 26 недели.
Этап 2.При вычисленни 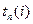 перемещаемся от завершающего события 7, к исходному 1 по сетевому графику против стрелок.
перемещаемся от завершающего события 7, к исходному 1 по сетевому графику против стрелок.
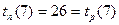 .
.
Далее рассматриваем непосредственно предшествующее событие 6, из которого выходит только одна работа (6, 7 или I):
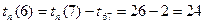 .
.
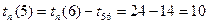 .
.
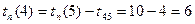 .
.
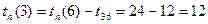 .
.
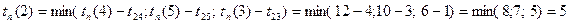 .
.
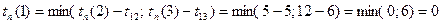 .
.
Этап 3.По формуле вычисляем резервы времени события i ,т.е. из чисел, полученных на этапе 2 вычитаем числа, полученные на этапе 1.
вычисляем резервы времени события i ,т.е. из чисел, полученных на этапе 2 вычитаем числа, полученные на этапе 1.
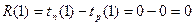 .
.
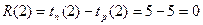 .
.
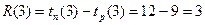 .
.
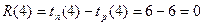 .
.
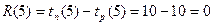 .
.
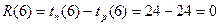 .
.
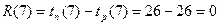 .
.
Для события 3 резерв времени составляет 3 недели. Это означает, что работа “В” можно задерживать до 3 недели, и этот задержка ни как не влияет на общую продолжительность проекта.
Этап 4.У критических событий резервы времени равен нулю, так как ранние и поздние сроки их свершения совпадают. Критическими событиями являются 1, 2, 4, 5, 6, 7 и определяют критический путь A, E, F, G, I, который на сетевом графике отмечены жирными линиями.
Теперь можно ответить на вопросы задачи.
На критическом пути находится работы A, E, F, G, I. Для завершения проекта потребуется 26 недели. Не возможно отложить начало выполнения работы Е поскольку она находится на критическом пути (срок выполнения проекта увеличится). Начало выполнения работы В можно отложить на 3 недели. На 3 недели можно отложить начало выполнения работы С. Это не изменить наиболее поздний срок наступления последующего события.
Вопросы
Вопрос 1. Метод СРМ разработан для:
1) описания проектов путем указания всех работ, предшествующих данной работе;
2) описания проектов путем представления каждой работы в виде пары узлов сети;
3) минимизации издержек на сокращение продолжительности проекта;
4) нахождения критического пути для проектов с заданным временем выполнения каждой работы;
5) нахождения критического пути для проектов с неопределенным временем выполнения работ.
Вопрос 2. Узел-событие сетевого графика выражает результат:
1) начаты все работы, выходящие из узла;
2) закончены все работы, входящие в узел;
3) начата хотя бы одна работа, выходящая из узла;
4) закончена хотя бы одна работа, входящая в узел;
5) закончены все работы, входящие в узел, и начата хотя бы одна работа, выходящая из узла.
Вопрос 3. Наиболее раннее время наступления события равно:
1) минимальной длине пути из данного узла в конечный;
2) максимальной длине пути из данного узла в конечный;
3) максимальной длине пути из начального узла в данный;
4) максимальному времени наиболее раннего окончания работ, входящих в данный узел;
5) минимальному времени наиболее позднего начала работ, выходящих из данного узла.
Вопрос 4. Наиболее позднее время наступления события равно:
1) Минимальной длине пути из данного узла в конечный;
2) максимальной длине пути из данного узла в конечный;
3) максимальной длине пути из начального узла в данный;
4) максимальному времени наиболее раннего начала работ, выходящих из данного узла;
5) минимальному времени наиболее позднего начала работ, выходящих из данного узла.
Вопрос 5. Для того чтобы сократить время выполнения проекта, необходимо:
1) сократить время выполнения каждой работы на критическом пути;
2) сократить время выполнения одной работы на критическом пути;
3) сократить время выполнения каждой работы проекта;
4) сократить время выполнения одной работы проекта;
5) увеличить длину критического пути.
Вопрос 6. Полный резерв времени выполнения работы равен разности между:
1) наиболее поздним и наиболее ранним временем ее начала;
2) наиболее ранним временем ее начала и наиболее ранним временем ее окончания;
3) наиболее поздним временем ее начала и наиболее поздним временем ее окончания;
4) наиболее ранним временем ее окончания и наиболее поздним временем ее начала;
5) наиболее поздним временем ее окончания и наиболее ранним временем ее начала.
Задачи
Задача 1. Экономический факультет МГУ разрабатывает новую программу для повышения квалификации преподавателей, обучающих количественным методам анализа экономики. Желательно, чтобы эту программу можно было реализовать в наиболее сжатые сроки.
Имеются существенные взаимосвязи между дисциплинами, которые необходимо отразить, составляя расписание занятий. Например, методы управления проектами PERТ/ СРМ должны рассматриваться лишь после того, как слушатели обсудят различные аспекты (коммерческие, финансовые, экономические, технические и др.) проектного анализа, связанные с жизненным циклом проекта.
Дисциплины и их взаимосвязь указаны в следующей таблице:
| Дисциплина | Опорные дисциплины | Время изучения, дни |
| A | - | |
| B | - | |
| C | A | |
| D | A | |
| E | C,B | |
| F | C,B | |
| G | F,D,E |
Найдите минимальное время, за которое можно выполнить программу.
Вопросы:
1. Какова длина критического пути?
2. Какое количество дисциплин находится на критическом пути?
3. Каков резерв времени изучения дисциплины f?
Задача 2. Консалтинговая компания «Системы управленческих решений» специализируется на разработке систем поддержки проектов. Компания заключила контракт на разработку компьютерной системы, предназначенной для помощи руководству фирмы при планировании капиталовложений.
Руководитель проекта разработал следующий перечень взаимосвязанных работ:
| Работа | Опорные работы | Время изучения, недели |
| A | - | |
| B | - | |
| C | - | |
| D | B | |
| E | A | |
| F | B | |
| G | C,D | |
| H | B,E | |
| I | F,G | |
| J | H,I |
Постройте графическое представление проекта. Используйте метод СРМ для нахождения критического пути.
Вопросы:
1. Какова длина критического пути?
2. Сколько работ находится на критическом пути?
3. Каков резерв выполнения работы F?
Задача 3. Рассмотрите следующий проект:
| Работа | Опорные работы | Время выполнения, недели |
| A | - | |
| B | - | |
| C | A | |
| D | A | |
| E | B | |
| F | D,E | |
| G | D,E | |
| H | G,C,F |
Найдите критический путь.
Вопросы:
1. За какое минимальное время может быть выполнен проект?
2. Сколько работ находится на критическом пути?
3. На сколько недель можно отложить выполнение работы D без отсрочки завершения проекта в целом?
4. На сколько недель можно отложить выполнение работы С без отсрочки завершения проекта в целом?
Задача 4. Проект пуско-наладки компьютерной системы состоит из восьми работ. Непосредственно предшествующие работы и продолжительность выполнения работ указаны в следующей таблице:
| Работа | Опорные работы | Время выполнения, недели |
| A | - | |
| B | - | |
| C | A | |
| D | B,C | |
| E | D | |
| F | E | |
| G | B,C | |
| H | F,G |
Найдите критический путь.
Вопросы:
1. Сколько времени потребуется для выполнения проекта?
2. Сколько работ на критическом пути?
3. Чему равно наиболее раннее время начала работы С?
4. На сколько дней можно отложить выполнение работы С без отсрочки завершения проекта в целом?
5. Чему равно наиболее позднее время окончания работы F?
6. На сколько дней можно отложить выполнение работы F без отсрочки завершения проекта?
Задача 5. Московский государственный университет рассматривает предложение о строительстве новой библиотеки. Работы, которые следует выполнить перед началом строительства, представлены ниже:
| Работа | Содержание работы | Опорные работы | Время выполнения, недели |
| A | Определить место строительство | - | |
| B | Разработать первоначальный проект | - | |
| C | Получить разрешение на строительство | A,B | |
| D | Выбрать архитектурную мастерсткую | C | |
| E | Разработать смету затрат на строительству | C | |
| F | Разработать проект строительство | D, E | |
| G | Обеспечить финансирования проекта | E | |
| H | Нанять подрядчика | F,G |
Найдите критический путь.
Вопросы:
1. Сколько работ находится на критическом пути? (Фиктивные работы не учитываются.)
2. Через какое минимальное время после принятия решения о реализации проекта можно начать работу по строительству библиотеки?
3. На сколько недель можно отложить выбор архитектурной мастерской?
4. Чему равно наиболее позднее время завершения работы по обеспечению финансирования?
Литература
4. Таха. Введение в исследовании операций. м.,1975.
6.1. Конспект лекции по дисциплиу управление проектами, разработанной доцентом Г.А. Беллуяном. Ереван, 2015г.
6.2. И.И. Мазур, В.Д. Шапиро, Н.Г. Ольдерогге, А.В. Полковников. Управление проектами. Москва, 2010г.
6.3. Г.И.Просветов. Математические методы в экономике. М.: 2005г.
6.4. Д. Филипс, А. Гарсиа-Диас. Методы анализа сетей. М. 1984г.
6.5. Конспект лекции по сетевого планирование и управление. Доцент, Беллуян Г.А.Ереван, 2014г.
6.6. Таха. Введение в исследовании операций. М.,1975.
6.7. Шапкин А.С. Математические методы и модели исследования операций. М., 2006г.
Тема 5. Сетевой анализ проектов. Метод СРМ. Лек. 7.
Критический путь
Временные параматри
Основные виды резервы времени
Основные формы расчета параметров сети
Построение сетевого графика в масштабе времени
Дата добавления: 2015-02-19; просмотров: 3434;
