Уравнение состояния реальных газов

В реальных газах вотличие от идеальных существенны силы межмолекулярных взаимодействий (силы притяжения, когда молекулы находятся на значительном расстоянии, и силы отталкивания при достаточном сближении их друг с другом) и нельзя пренебречь собственным объемом молекул.

Наличие межмолекулярных сил отталкивания приводит к тому, что молекулы могут сближаться между собой только до некоторого минимального расстояния. Поэтому можно считать, что свободный для движения молекул объем будет равен , где b — тот наименьший объем, до которого можно сжать газ. В соответствии с этим длина свободного пробега молекул уменьшается и число ударов о стенку в единицу времени, а следовательно, и давление увеличивается по сравнению с идеальным газом в отношении

,

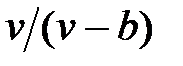т. е.

.

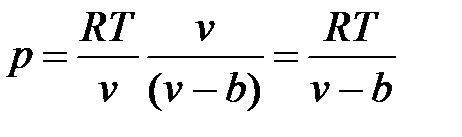Силы притяжения действуют в том же направлении, что и внешнее давление, и приводят к возникновению молекулярного (или внутреннего) давления. Сила молекулярного притяжения каких-либо двух малых частей газа пропорциональна произведению числа молекул в каждой из этих частей, т. е. квадрату плотности, поэтому молекулярное давление обратно пропорционально квадрату удельного объема газа: р_мол = а/v², где а — коэффициент пропорциональности, зависящий от природы газа.

Отсюда получаем уравнение Ван-дер-Ваальса (1873 г.):

,

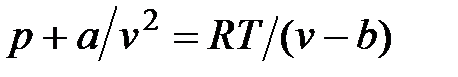или

.

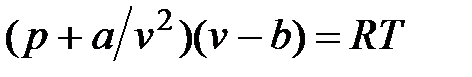При больших удельных объемах и сравнительно невысоких давлениях ре­ального газа уравнение Ван-дер-Ваальса практически вырождается в уравнение состояния идеального газа Клапейрона, ибо величина a/v² (по сравнению с p) и b (по сравнению с v) становятся пренебрежимо малыми.

Уравнение состояния газа Ван-дер-Ваальса - уравнение состояния, описывающее свойства реального газа. Предложено Й. Д. Ван-дер-Ваальсом в 1873 г. Широко используется для качественного анализа поведения реальных газов и жидкостей. В модели реального газа Ван-дер-Ваальса молекулы рассматриваются как абсолютно твердые слабо притягивающиеся упругие сферы определенного диаметра.

Уравнение Ван-дер-Ваальса количественно определяет свойства реальных газов лишь в небольшом интервале температур и давлений: в области относительно высоких температур и низких давлений, так как входящие в него экспериментально определяемые константы являются функциями температуры.

Для моля газа объемом V при температуре Т и давлении р, уравнение Ван-дер-Ваальса имеет вид:

(p+a/V_m ²)(V_m- b) = RT,

где: R — газовая постоянная,

a и b — экспериментальные константы, учитывающие отклонение свойств реального газа от свойств идеального газа.

Член a/V² имеет размерность давления и учитывает притяжение между молекулами газа за счет ван-дер-ваальсовых сил. Действие сил притяжения газа приводит к появлению дополнительного давления на газ, называемого внутренним давлением. По вычислениям Ван-дер-Ваальса, внутреннее давление обратно пропорционально квадрату молярного объема, т. е. р_вн= a/V_m², где а — постоянная Ван-дер-Ваальса, характеризующая силы межмолекулярного притяжения, V_m — молярный объем.

Константа b является поправкой на собственный объем молекул газа и учитывает отталкивание молекул на близких расстояниях. Наличие сил отталкивания, которые противодействуют проникновению в занятый молекулой объем других молекул, приводит к тому, что фактически свободный объем, в котором будут двигаться молекулы реального газа, будет не V _m, а V _m-b, где b — объем, занимаемый самими молекулами. Объем b равен учетверенному собственному объему молекул.

Константы а и b обычно определяются из экспериментальных данных, и эти величины постоянны для каждого газа. Для их определения записывают уравнения для двух известных из опыта состояний газа и решают эти уравнения относительно а и b. При больших объемах V можно пренебречь обеими поправками и уравнение Ван-дер-Ваальса переходит в уравнение состояния идеального газа (см. Клапейрона уравнение).

Несмотря на то, что уравнение Ван-дер-Ваальса является приближенным и количественно описывает свойства реальных газов лишь в области высоких температур и низких давлений, качественно оно позволяет описывать поведение газа и при высоких давлениях, конденсацию газа в жидкость. Уравнение Ван-дер-Ваальса также описывает критическое и метастабильное состояние системы жидкость-пар.

Уравнение Ван-дер-Ваальса с качественной стороны достаточно хорошо описывает свойства реального газа, но результаты численных расчетов не всегда согласуются с экспериментальными данными. В ряде случаев эти отклонения объясняются склонностью молекул реального газа к ассоциации в отдельные группы, состоящие из двух, трех и более молекул. Ассоциация происходит вследствие несимметричности внешнего электрического поля молекул. Образовавшиеся комплексы ведут себя как самостоятельные нестабильные частицы. При столкновениях они распадаются, затем вновь объединяются уже с другими мо­лекулами и т. д. По мере повышения температуры концентрация комплексов с большим числом молекул быстро уменьшается, а доля одиночных молекул растет. Большую склонность к ассоциации проявляют полярные молекулы водяного пара.