Лекция 2.
Термодинамические процессы. Идеальные газы и их смеси.Термодинамический процесс.
Изменение состояния термодинамической системы во времени называется термодинамическим процессом. Так, при перемещении поршня в цилиндре объём, а с ним давление и температура находящегося внутри газа будут изменяться, будет совершаться процесс расширения или сжатия газа.
Как уже отмечалось, система, выведенная из состояния равновесия, и предоставленная при постоянных параметрах окружающей среды самой себе, через некоторое время вновь придет в равновесное состояние, соответствующее этим параметрам. Такое самопроизвольное (без внешнего воздействия) возвращение системы в состояние равновесия называется релаксацией, а промежуток времени, в течение которого система возвращается в состояние равновесия, называется временем релаксации. Для разных процессов оно различно: если для установления равновесного давления в газе требуется всего 10 с, то для выравнивания температуры в объеме того же газа нужны десятки минут, а в объеме нагреваемого твердого тела - иногда несколько часов.
Термодинамический процесс называется равновесным, если все параметры системы при его протекании меняются достаточно медленно по сравнению с соответствующим процессом релаксации. В этом случае система фактически все время находится в состоянии равновесия с окружающей средой, чем и определяется название процесса.
Чтобы процесс был равновесным, скорость изменения параметров системы 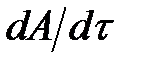 должна удовлетворять соотношению:
должна удовлетворять соотношению:
 ,
,
где A — параметр, наиболее быстро изменяющийся в рассматриваемом процессе; cрел — скорость изменения этого параметра в релаксационном процессе; τрел — время релаксации.
Рассмотрим, например, процесс сжатия газа в цилиндре. Если время смещения поршня от одного положения до другого существенно превышает время релаксации, то в процессе перемещения поршня давление и температура успеют выровняться по всему объему цилиндра.
Это выравнивание обеспечивается непрерывным столкновением молекул, в результате чего подводимая от поршня к газу энергия достаточно быстро и равномерно распределяется между ними. Если последующие смещения поршня будут происходить аналогичным образом, то состояние системы в каждый момент времени будет практически равновесным. Таким образом, равновесный процесс состоит из непрерывного ряда последовательных состояний равновесия, поэтому в каждой его точке состояние термодинамической системы можно описать уравнением состояния данного рабочего тела. Именно поэтому классическая термодинамика в своих исследованиях оперирует только равновесными процессами. Они являются удобной идеализацией реальных процессов, позволяющей во многих случаях существенно упростить решение задачи. Такая идеализация вполне обоснована, так как условие выполняется на практике достаточно часто. Поскольку механические возмущения распространяются в газах со скоростью звука, процесс сжатия газа и цилиндре будет равновесным, если скорость перемещения поршня много меньше скорости звука.
Процессы, не удовлетворяющие условию 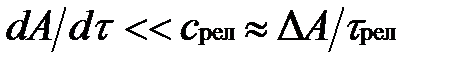 , протекают с нарушением равновесия, т. е. являются неравновесными. Если, например, быстро увеличит температуру окружающей среды, то газ в цилиндре будет постепенно прогреваться через его стенки, релаксируя к состоянию равновесия, соответствующему новым параметрам окружающей среды. В процессе релаксации газ не находится в равновесии с окружающей средой и его нельзя характеризовать уравнением состояния хотя бы потому, что в разных точках объема газа температура имеет различные значения.
, протекают с нарушением равновесия, т. е. являются неравновесными. Если, например, быстро увеличит температуру окружающей среды, то газ в цилиндре будет постепенно прогреваться через его стенки, релаксируя к состоянию равновесия, соответствующему новым параметрам окружающей среды. В процессе релаксации газ не находится в равновесии с окружающей средой и его нельзя характеризовать уравнением состояния хотя бы потому, что в разных точках объема газа температура имеет различные значения.
Идеальным газомназывается такой газ, у которого отсутствуют силы взаимного притяжения и отталкивания между молекулами и пренебрегают размерами молекул. Все реальные газы при высоких температурах и малых давлениях можно практически считать как идеальные газы.
Уравнение состояния как для идеальных, как и для реальных газов описываются тремя параметрами по уравнению
f (Р, v, Т) = 0.
Уравнение состояния идеального газа можно вывести из молекулярно-кинетической теории или из совместного рассмотрения законов Бойля-Мариотта и Гей-Люссака.
Это уравнение было выведено в 1834 г. французским физиком Клапейроном и для 1 кг массы газа имеет вид:
P*v = R·Т,
где: R - газовая постоянная и представляет работу 1 кг газа в процессе при постоянном давлении и при изменении температуры на 1 градус.
Уравнение cp - cv = R - уравнение Майера называют термическим уравнением состояния или характеристическим уравнением.
Для произвольного количества газа массой m уравнение состояния будет:
Р·V = m*R*T .
В 1874 г. Д.И.Менделеев основываясь на законе Дальтона ("В равных объемах разных идеальных газов, находящихся при одинаковых температурах и давлениях, содержится одинаковое количество молекул") предложил универсальное уравнение состояния для 1 кг газа, которую называют уравнением Клапейрона-Менделеева:
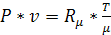 ,
,
где:  - молярная (молекулярная) масса газа, (кг/кмоль);
- молярная (молекулярная) масса газа, (кг/кмоль);
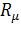 = 8314,20 Дж/кмоль (8,3142 кДж/кмоль) - универсальная газовая постоянная и представляет работу 1 кмоль идеального газа в процессе при постоянном давлении и при изменении температуры на 1 градус.
= 8314,20 Дж/кмоль (8,3142 кДж/кмоль) - универсальная газовая постоянная и представляет работу 1 кмоль идеального газа в процессе при постоянном давлении и при изменении температуры на 1 градус.
Зная Rμ можно найти газовую постоянную:
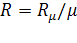 .
.
Для произвольной массы газа уравнение Клапейрона-Менделеева будет иметь вид:
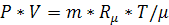 .
.
Все зависимости, полученные выше для идеальных газов, справедливы и для их смесей, если в них подставлять газовую постоянную, молекулярную массу и теплоемкость смеси.
Закон Дальтона.В инженерной практике часто приходится иметь дело с газообразными веществами, близкими по свойствам к идеальным газам и представляющими собой механическую смесь отдельных компонентов различных газов, химически не реагирующих между собой. Это так называемые газовые смеси. В качестве примера можно назвать продукты сгорания топлива в двигателях внутреннего сгорания, топках печей и паровых котлов, влажный воздух в сушильных установках и т. п.
Основным законом, определяющим поведение газовой смеси, является закон Дальтона: полное давление смеси идеальных газов равно сумме парциальных давлений всех входящих в нее компонентов:
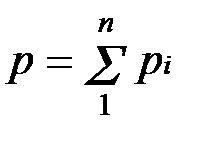
Парциальное давление pi — давление, которое имел бы газ, если бы он один при той же температуре занимал весь объем смеси.
Способы задания смеси.Состав газовой смеси может быть задан массовыми, объемными или мольными долями.
Массовой долей называется отношение массы отдельного компонента Мi, к массе смеси М:
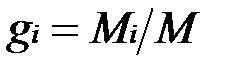 ,
,
Очевидно, что 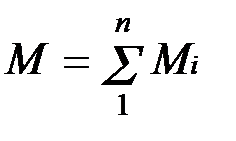
 и
и 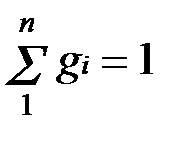 .
.
Массовые доли часто задаются в процентах. Например, для сухого воздуха 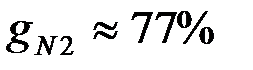 ;
; 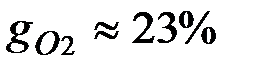 .
.
Объемная доля представляет собой отношение приведенного объема газа V, к полному объему смеси V:
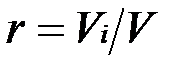 .
.
Приведенным называется объем, который занимал бы компонент газа, если бы его давление и температура равнялись давлению и температуре смеси.
Для вычисления приведенного объема запишем два уравнения состояния i-го компонента:
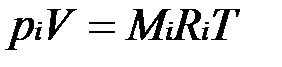 ; (2.1)
; (2.1)
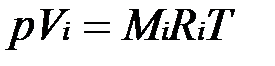 .
.
Первое уравнение относится к состоянию компонента газа в Смеси, когда он имеет парциальное давление pi и занимает полный объем смеси, а второе уравнение — к приведенному состоянию, когда давление и температура компонента равны, как и для смеси, р и Т. Из уравнений следует, что
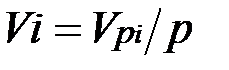 , (2.2)
, (2.2)
Просуммировав соотношение (2.2) для всех компонентов смеси, получим с учетом закона Дальтона 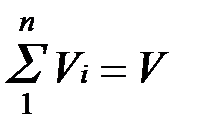 ,откуда
,откуда 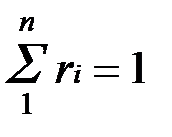 . Объемные доли также часто задаются в процентах. Для воздуха
. Объемные доли также часто задаются в процентах. Для воздуха 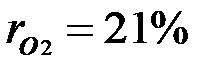 ,
, 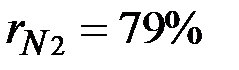 .
.
Иногда бывает удобнее задать состав смеси мольными долями. Мольной долей называется отношение количества молей Ni рассматриваемого компонента к общему количеству молей смеси N.
Пусть газовая смесь состоит из N1 молей первого компонента, N2 молей второго компонента и т. д. Число молей смеси 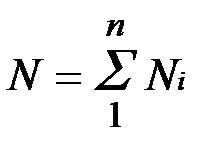 , а мольная доля компонента будет равна
, а мольная доля компонента будет равна 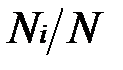 .
.
В соответствии с законом Авогадро объемы моля любого газа при одинаковых p и T, в частности при температуре и давлении смеси, в идеально газовом состоянии одинаковы. Поэтому приведенный объем любого компонента может быть вычислен как произведение объема моля 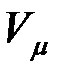 на число молей этого компонента, т. е.
на число молей этого компонента, т. е. 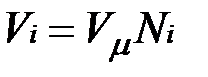 а объем смеси — по формуле
а объем смеси — по формуле 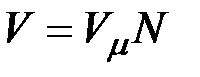 . Тогда
. Тогда 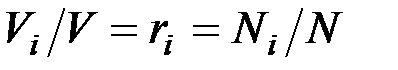 , и, следовательно, задание смесильных газов мольными долями равно заданию ее объемными долями.
, и, следовательно, задание смесильных газов мольными долями равно заданию ее объемными долями.
Газовая постоянная смеси газов. Просуммировавуравнения (2.1) для всех компонентов смеси, получим  . Учитывая
. Учитывая 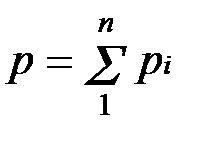 , можно записать:
, можно записать:
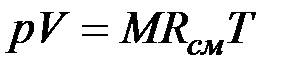 , (2.3)
, (2.3)
где
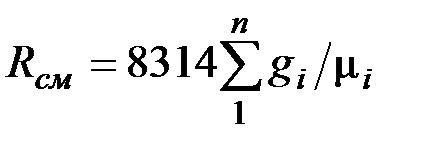 . (2.4)
. (2.4)
Из уравнения (2.3) следует, что смесь идеальных газов также подчиняется уравнению Клапейрона. Поскольку 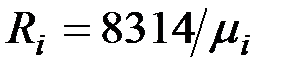 то из (2.4) следует, что газовая постоянная смеси [Дж/(кг-К)] имеет вид
то из (2.4) следует, что газовая постоянная смеси [Дж/(кг-К)] имеет вид
 , (2.5)
, (2.5)
Кажущаяся молекулярная масса смеси. Выразим формально газовую постоянную смеси R, введя кажущуюся окулярную массу смеси 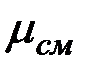 :
:
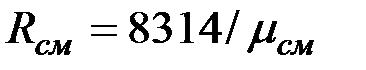 , (2.6)
, (2.6)
Сравнивая правые части соотношений (2.5) и (2.6), найдем:
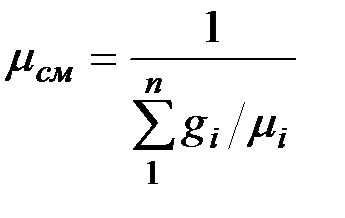 .
.
Изопределения массовых долей следует, что
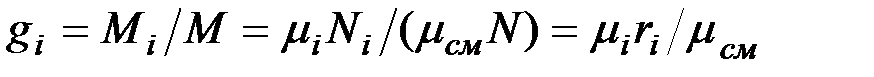
Просуммировав это соотношение, для всех компонентов и учитывая, что 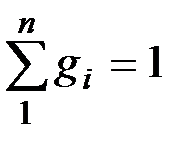 , получим выражение для кажущейся молекулярной и массы смеси, заданной объемными долями:
, получим выражение для кажущейся молекулярной и массы смеси, заданной объемными долями:
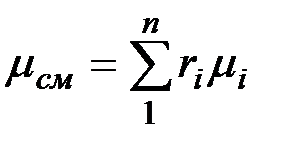 , (2.7)
, (2.7)
Соотношение между объемными и массовыми долями. Учитывая (2.7), получаем 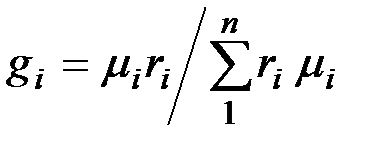 .
.
Поскольку 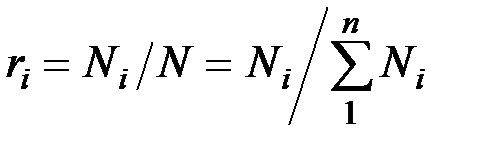 , то
, то
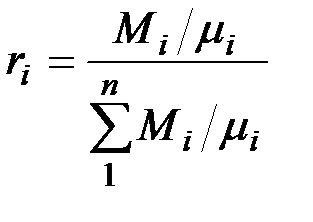
Разделив числитель и знаменатель этой формулы на массу смеси М, получим
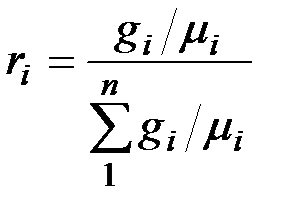 .
.
Дата добавления: 2015-02-16; просмотров: 1009;
