Устойчивость систем со звеном чистого запаздывания

Системы со звеньями чистого запаздывания относятся к иррациональным системам, поэтому они не поддаются анализу алгебраическими критериями устойчивости. Наиболее применимый метод анализа – частотный метод (метод Найквиста).

Характеристическое уравнение такой системы:

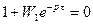
Предположим, что разомкнутая система – устойчивая. Звено чистого запаздывания не вносит изменений по амплитуде, а изменяет только фазу.

Графически это означает поворот любой точки годографа амплитудно-фазовой характеристики разомкнутой системы на угол 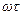по часовой стрелке.

Поскольку при 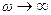амплитуда достаточно мала, то годограф амплитудно-фазовой характеристики всей системы (т.е. со звеном чистого запаздывания) закручивается вокруг начала координат

.

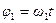Строится годограф системы со звеном чистого запаздывания. Определяется точка пересечения данного годографа с окружностью единичного радиуса, и соответствующая данной точке частота. Берется запас устойчивости s и определяется величина tw_p.

Вывод: звено чистого запаздывания ухудшает характеристики по отношению к устойчивости и может возникнуть такая ситуация, что при времени чистого запаздывания t₀ годограф пересечет т.[-1,0], т.е. меняя t,мы можем выводить систему на устойчивое состояние:

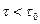- система устойчивая;

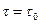- система на границе устойчивости;

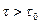- система неустойчива.

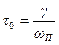или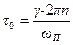

Здесь t₀ - критическое время чистого запаздывания.

Кроме того, звено чистого запаздывания уменьшает запас устойчивости системы.