Потенциальная диаграмма

Для экспериментального подтверждения и наглядной иллюстрации второго закона Кирхгофа построим потенциальную диаграмму, которая представляет собой график распределения потенциала вдоль какого-либо участка цепи или контура. По оси абсцисс на нем откладывают в масштабе отрезки, соответствующие сопротивлениям вдоль контура, начиная с какой-либо произвольной точки, а по оси ординат − потенциалы соответствующих точек контура относительно точки, потенциал которой принят за нулевой.

Рассмотрим контур электрической цепи, изображенный на рис.1.3, и построим для него потенциальную диаграмму. Для этого зададим направление обхода контура по часовой стрелке и примем потенциал точки a равным нулю: φ_a= 0.

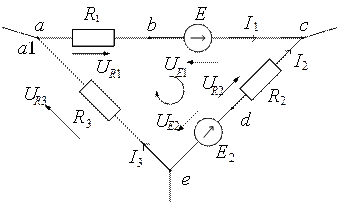
Рис. 1.3. Контур электрической цепи

Для потенциалов соответствующих точек схемы согласно выражениям (1.1)...(1.4) справедливы следующие соотношения:

φ_b= φ_a−I₁R₁= − I₁R₁;

φ_c= φ_b +E₁ = − I₁R₁+ E₁;

φ_d= φ_c + I₂R₂ = − I₁R₁+ E₁ + I₂R₂;

φ_e= φ_d − E₂ = − I₁R₁+ E₁ + I₂R₂ − E₂;

φ_a1= φ_e − I₃R₃ = − I₁R₁+ E₁ + I₂R₂ − E₂ −I₃R₃,

где φ_a1 - потенциал точки a, выраженный через напряжения на элементах контура.

Обходя контур по часовой стрелке, мы пришли в ту же точку a (a1), из которой начали движение. Разность потенциалов φ_a и φ_a1, очевидно, равна нулю, т.е.

φ_a− φ_a1 = I₁R₁−E₁ − I₂R₂ + E₂ +I₃R₃=0. (1.9)

В обозначениях напряжений на элементах контура выражение (1.9) принимает вид:

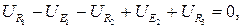(1.10)

что соответствует уравнению (1.7) для ЗНК.

Перенеся ЭДС в правую часть равенства (1.9), получим:

I₁R₁− I₂R₂ +I₃R₃ = E₁− E₂, (1.11)

что соответствует уравнению (1.8) для ЗНК.

Потенциальная диаграмма в виде зависимости φ(R) приведена на рис.1.4. Пользуясь потенциальной диаграммой, можно найти разность потенциалов между любыми точками электрической цепи.

Рис.1.4. Потенциальная диаграмма

Правильность расчета электрической цепи можно проверить по балансу мощности, согласно которому суммарная мощность, генерируемая источниками, равна суммарной мощности, потребляемой в цепи:

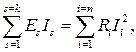(1.12)

где k − количество источников ЭДС в схеме; n − количество приемников (активных сопротивлений).