Законы Кирхгофа. При расчете и анализе электрических цепей изначально необходимо задаться положительным направлением токов в ветвях

При расчете и анализе электрических цепей изначально необходимо задаться положительным направлением токов в ветвях. В соответствии с принятыми положительными направлениями токов определяются и положительные направления напряжений на элементах цепи. В общем случае положительные направления токов задаются произвольно. Если в результате расчета получается отрицательное значение тока, то это значит, что данный ток в ветви направлен в противоположную сторону по сравнению с принятым положительным направлением.

Электрические цепи подразделяются на неразветвленные и разветвленные. В неразветвленной цепи во всех элементах течет один и тот же ток. В разветвленной цепи по каждой ветви течет свой ток.

Все электрические цепи подчиняются законам Кирхгофа. Их два.

Первый закон - закон токов Кирхгофа (ЗТК) устанавливает связь между токами в узле электрической схемы: алгебраическая сумма токов в любом узле равна нулю, т.е.

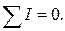(1.6)

При составлении уравнения (1.6) по первому закону Кирхгофа токи, направленные к узлу, следует брать со знаком, противоположным знаку токов, направленных от узла.

Второй закон - закон напряжений Кирхгофа (ЗНК) устанавливает связь между напряжениями в контуре электрической цепи: алгебраическая сумма напряжений на всех элементах вдоль любого контура равна нулю, т.е.

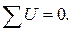(1.7)

В выражении (1.7) падения напряжения, совпадающие с направлением обхода контура, берутся со знаком "плюс", а ЭДС, совпадающие с направлением обхода контура, − со знаком "минус", например, как в выражении (1.3), поскольку напряжение на источнике ЭДС направлено встречно самой ЭДС (в соответствии с направлением стрелки Е).

Для того, чтобы исключить возможные ошибки при определении знаков слагаемых в (1.7), все ЭДС из левой части уравнения целесообразно перенести в правую часть. Тогда второй закон Кирхгофа может быть сформулирован иначе: алгебраическая сумма падений напряжения в любом контуре равняется алгебраической сумме ЭДС, действующих в том же контуре, т.е.

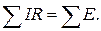(1.8)

В этом случае в каждую из сумм в уравнении (1.8) соответствующие слагаемые (как падения напряжения в левой части, так и ЭДС в правой) входят со знаком "плюс", если совпадают с направлением обхода контура, и со знаком "минус", если не совпадают с ним.