МЕТОДОМ МАГНЕТРОНА

1. Быстрицкий Г.Ф. Основы энергетики: Учебник. – М.: ИНФРА – М, 2005.

2. Липов Ю.М., Третьянов Ю.М. Котельные установки и парогенераторы. – Москва – Ижевск: НИЦ «Регулярная и хаотическая динамика», 2003.

3. Стерман Л.С., Лавыгин В.М., Тишин С.Г. Тепловые и атомные электрические станции. – М: Издательство МЭИ, 2004.

ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО ЗАРЯДА ЭЛЕКТРОНА

МЕТОДОМ МАГНЕТРОНА

1.1. Теоретические сведения

В основе определения удельного заряда электрона методом магнетрона лежит тот факт, что электрически заряженная частица, движущаяся в магнитном поле, изменяет направление своего движения.

Магнетрон – это прибор для генерации электромагнитных колебаний СВЧ, которые используются в радиолокационных устройствах. Анод магнетрона выполнен в виде набора резонаторных камер, размер которых определяет длину волны возбуждаемых электромагнитных колебаний при взаимодействии электронов, движущихся в магнитном поле от катода к аноду по криволинейным траекториям. При попадании на анод электроны тормозятся, отдавая свою энергию электромагнитному полю, которое возбуждается в резонаторах анода. Магнетроны способны генерировать колебания мощностью до тысячи кВт в импульсном режиме вплоть до миллиметрового диапазона электромагнитных волн, которые по специальным устройствам – волноводам направляются к антеннам передающих устройств.

Экспериментально установлено, что на частицу с электрическим зарядом 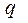, движущуюся со скоростью 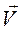в магнитном поле с индукцией 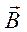,действует сила Лоренца

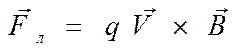(1)

Из (1) следует, что направление действия этой силы всегда перпендикулярно вектору скорости частицы. Как известно из механики, в этом случае модуль скорости движения тела измениться не может. Значит, ускорение, которое сообщает заряженному телу сила Лоренца, определяет изменение вектора скорости только по направлению, а это приводит к искривлению траектории его движения.

Изменить модуль скорости заряженной частицы можно только за счёт работы сил электрического поля. При помещении заряженной частицы в электрическое поле с напряжённостью 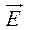на неё действует кулоновская сила

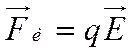, (2)

под действием которой частица приобретает ускорение. Изменение кинетической энергии такой частицы равно работе кулоновской силы независимо от наличия магнитного поля. При отсутствии начальной скорости у частицы изменение её кинетической энергии определяется по формуле:

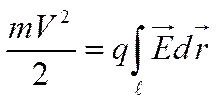(3)

Учитывая связь между вектором напряжённости и потенциалом электрического поля, работу сил поля по перемещению заряда вдоль траектории 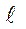можно вычислить по формуле

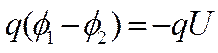(4)

В (4) 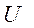- напряжение между точками поля с потенциалам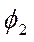и и .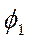

Итак, для целей нашего эксперимента необходимо с помощью электрического поля заставить электрон двигаться с некоторой скоростью в магнитном поле. Если векторы 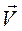и 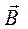будут взаимно перпендикулярны, то траекторией движения заряженной частицы будет плоская кривая. Осуществить эти условия можно в ламповом диоде - двухэлектродной лампе, помещённой во внешнее магнитное поле. Электроды диода – подогреваемый катод и холодный анод выполнены в виде коаксиальных цилиндров. Как и в цилиндрическом конденсаторе, в межэлектродном пространстве диода имеется только радиальное распределение напряжённости электрического поля

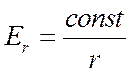(5)

Магнитное поле создаётся током, протекающим в катушке соленоида, соосной с коаксиальными электродами лампы. Электроны, вылетающие вследствие термоэлектронной эмиссии с катода, попадают в скрещенные под прямым углом электрическое и магнитное поля. Если диод работает в режиме насыщения, то при отсутствии магнитного поля все электроны двигаются по прямым траекториям в радиальных направлениях от катода к аноду. При включении магнитного поля сила Лоренца отклоняет электроны от прямолинейной траектории. Радиус кривизны траектории движения электрона зависит от величины модуля вектора магнитной индукции, при этом до достижения некоторого критического значения 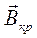электроны всё же достигают анода и анодный ток через лампу не изменяется.

При 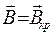траектория движения электрона искривится настолько, что только коснётся цилиндрической поверхности анода, при дальнейшем увеличении магнитного поля электрон вовсе не попадёт на анод и ток в анодной цепи лампы прекращается. Значение индукции 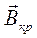и соответствующее ему значение тока в соленоиде 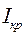называются критическими значениями для данного анодного напряжения.

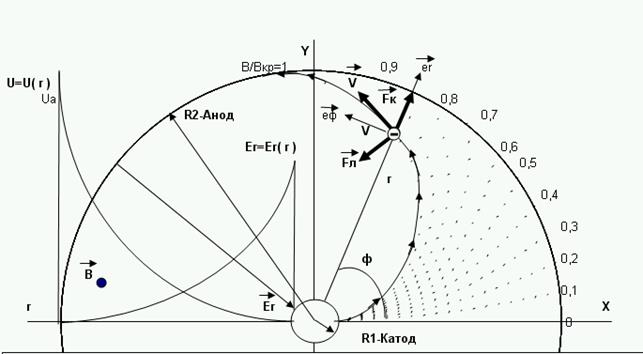
Движение электрона в межэлектродном пространстве.

Рис.1

На рис.1 показаны траектории движения электронов в межэлектродном пространстве магнетрона, полученные численным интегрированием зависимости полярного угла 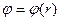при различных значениях 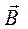, сплошная линия со стрелками – «критическая траектория».

1.2. Основные элементы теоретической модели физики процессов

Из теоретического введения ясно, что электрон, движущийся в межэлектродном пространстве лампового диода, испытывает воздействие обоих полей - и электрического и магнитного одновременно!

Для вывода формулы будем исходить из реальных представлений о физике процессов, с учётом следующих предположений:

1) влияние силы тяжести учитывать не будем;

2) 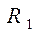- внешний радиус катода, 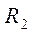- внутренний радиус анода лампового диода;

3) вследствие термоэлектронной эмиссии все электроны покидают катод с одинаковыми начальными условиями (без начальной скорости), в этом смысле все электроны идентичны;

4) в отсутствие постоянного магнитного поля, в ускоряющем электрическом поле все электроны двигаются прямолинейно в параллельных плоскостях, распределяясь равномерно во всех радиальных направлениях, т.е. диод работает в режиме насыщения;

5) в кольцевом пространстве между анодом и катодом распределение напряжённости электрического поля является функцией только расстояния, отсчитываемого от оси катода (формула 4);

6) магнитное поле однородное и вектор магнитной индукции направлен по оси лампы вверх;

7) при критическом значении модуля магнитной индукции траектория движения электрона касается внутренней поверхности цилиндрического анода.

При этих условиях по достижении модуля магнитной индукции критического значения ток через магнетрон должен мгновенно прекратиться. В реальном эксперименте с диодом условия 3), 4), 5) и 6) не выполняются, поэтому анодный ток через лампу мгновенно не прекращается, а падает до нуля в некотором диапазоне значений тока в соленоиде. За критическое значение тока в соленоиде целесообразно принимать значение, соответствующее середине интервала резкого падения анодного тока.

С учётом высказанных выше предположений, решение задачи целесообразно проводить в цилиндрической системе координат 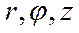(полюс на оси диода, ось 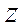- вверх, ось 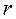- от оси диода к аноду). Интересующие нас векторы физических величин в этой системе координат будут иметь следующие проекции (рис.1):

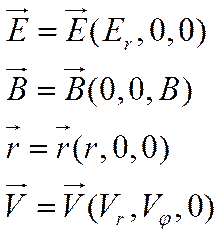(5а)

В (5) 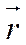- радиус- вектор точки в декартовой системе координат.

Формула для определения удельного заряда электрона получена двумя способами. В п.1.3 – с помощью закона об изменении кинетической энергии электрона и закона об изменении его момента импульса. В п.1.4 – на основе точного аналитического решения задачи о движении электрона в скрещенных электрическом и магнитном полях. Обе методики равноценны и дают правильный результат. Оба подхода позволяют получить аналитические выражения для радиальных распределений проекций мгновенной скорости и вывести интегральное соотношение для расчёта траектории движения .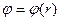

1.3. Энергетический подход и уравнение моментов

Запишем уравнение изменения кинетической энергии электрона (3) с учётом (4), разложив модуль вектора мгновенной скорости электрона на составляющие в цилиндрической системе координат и учитывая, что электрон имеет отрицательный заряд:

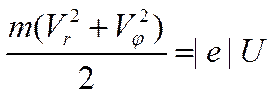, (6)

где:

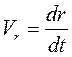- радиальная составляющая вектора скорости, (7)

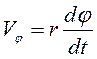- азимутальная составляющая вектора скорости. (8)

Это соотношение справедливо для любого момента времени, т.е. скорость электрона в произвольной точке межэлектродного пространства определяется напряжением между этой точкой и катодом.

Для электрона, движущегося в межэлектродном пространстве, можно записать ещё одно уравнение в соответствии с законом об изменении его момента импульса. Это уравнение называется уравнением моментов. В общем виде оно выглядит так:

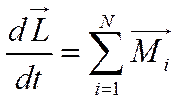(9)

В (9) момент импульса электрона относительно начала координат определяется как для материальной точки:

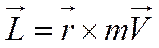, (10)

а моменты сил, действующих на электрон, также относительно начала координат вычисляются по определению:

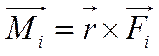(11)

Из допущений, сделанных в п.1.2, ясно, что на электрон действуют две силы – Лоренца (1) и Кулона (2). Эти силы в цилиндрической системе координат имеют следующие проекции:

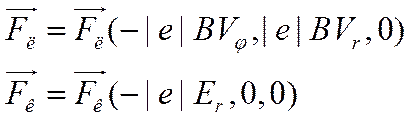(12)

Если с учётом (10), (11) и (12) спроецировать уравнение моментов (9) на цилиндрические оси координат (векторные произведения следует представлять в виде определителей третьего порядка и искать их алгебраические дополнения), то выяснится, что не сохраняется только момент импульса электрона относительно оси 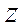. В результате, с учётом (6), получим систему из двух скалярных уравнений для нахождения удельного заряда электрона:

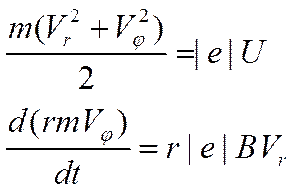(13)

Второе уравнение этой системы можно проинтегрировать. С учётом (7) получим:

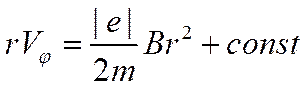
Неизвестную постоянную можно найти, учитывая граничные условия на катоде:

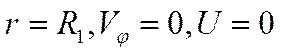(14)

Тогда выражение для азимутальной скорости электрона будет иметь вид:

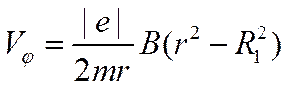(15)

Используя для первого уравнения системы (13) граничные условия на аноде при критическом значении магнитной индукции

В = В_кр , r = R₂ , V_r = 0, U = U_a , (16)

получим:

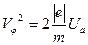
Подставив сюда значение азимутальной скорости из (15) при условии (16), получим формулу для определения удельного заряда электрона методом магнетрона:

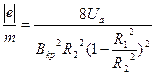(17)

1.4. Движение электрона в скрещенных полях

Формулу для расчёта удельного заряда электрона можно получить на основе аналитического решения задачи о движении электрона в скрещенных полях - радиальном электрическом и однородном магнитном.

На электрон, движущийся в межэлектродном пространстве лампового диода в скрещенных электрическом и магнитном полях, действует сила Кулона и сила Лоренца (рис.1). В векторной форме 2-й закон Ньютона для электрона можно записать в виде:

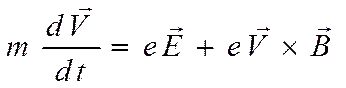, (18)

где:

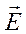- вектор напряжённости электрического поля,

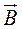- вектор магнитной индукции,

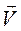- вектор мгновенной скорости электрона,

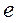- заряд электрона,

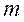- масса электрона.

В цилиндрической системе координат 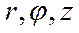векторы в (18) имеют проекции (рис.1) в соответствии с (5) и (12). Из этих условий следует, что уравнение (18) в цилиндрической системе координат не имеет проекции на ось Z . Поэтому траекторией движения электрона будет плоская кривая и решение можно продолжить в полярной системе координат.

При проецировании левой части уравнения (18) на полярные оси координат необходимо учесть, что для движущейся частицы орты полярной системы координат 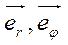изменяют свое положение на плоскости (рис.1).

Проецируя правую часть уравнения (18) на полярные оси координат, векторное произведение следует представить в виде определителя третьего порядка и найти его алгебраические дополнения. В результате получим систему из двух скалярных уравнений:

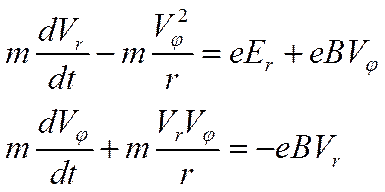, (19)

где:

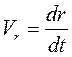- радиальная составляющая вектора скорости,

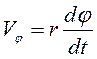- азимутальная составляющая вектора скорости,

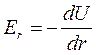- радиальная составляющая вектора напряжённости, (20)

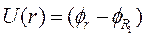- разность потенциалов (напряжение) между точкой в межэлектродном пространстве с радиусом 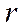и катодом с радиусом 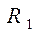. Учитывая, что электрон имеет отрицательный заряд и принимая во внимание соотношение (20), систему (19) можно переписать в виде:

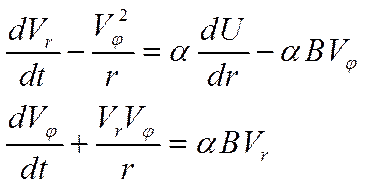, (21)

где введено обозначение 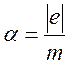- удельный заряд электрона.

Анализ системы (21) показывает, что второе уравнение оказывается тождественным второму уравнению в системе (13), т.е. уравнению моментов, из которого было найдено общее решение (15) для азимутальной скорости электрона на произвольном расстоянии от катода в межэлектродном пространстве. Остаётся найти радиальную компоненту скорости электрона. Для этого нужно преобразовать первое уравнение в системе (21). Перенесём в правую часть член уравнения, пропорциональный квадрату азимутальной скорости, а затем умножим и разделим левую часть этого уравнения на 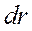.Учитывая (7), будем иметь:

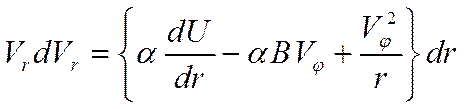(22)

Подставив в (22) решение для азимутальной компоненты (15), после интегрирования получим:

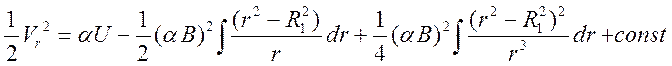
Вычислив интегралы в правой части этого выражения, получим общее решение для радиальной компоненты скорости электрона:

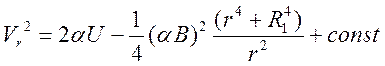
Неопределённую постоянную можно найти из граничного условия на катоде (14). Применив его, будем иметь:

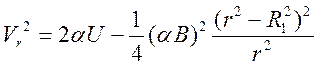(23)

Отметим, что выражение (23) тождественно закону изменения кинетической энергии электрона в виде (6), т.к. второй член есть не что иное, как квадрат азимутальной скорости. Если учесть в (23) граничные условия на аноде при критическом значении магнитной индукции (16), то в результате получим формулу (17).

Если радиальное распределение напряжённости электрического поля в межэлектродном пространстве соответствует формуле (5), то после интегрирования (20) с учётом граничных условий на аноде (16) радиальное распределение напряжения в диоде будет иметь вид:

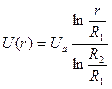(24)

Используя соотношения (7), (8), (15), (23) и (24), можно получить аналитическое выражение для зависимости 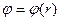в интегральном виде. Численное интегрирование позволяет построить траектории движения электрона в полярных координатах в скрещенных электрическом и магнитном полях (рис.1). На рис.2 представлены радиальные распределения безразмерных радиальной и азимутальной компонент скорости электрона в зависимости от значения магнитной индукции в диоде.

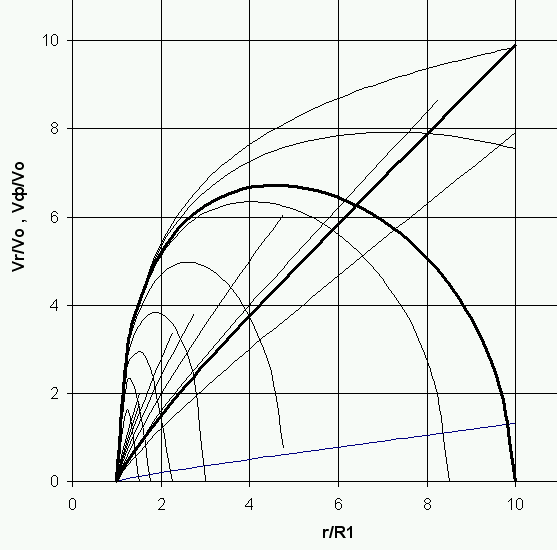
Радиальное распределение азимутальной и радиальной компонент

скорости электрона в зависимости от значения магнитной индукции.

Рис.2

Представленные данные рассчитаны по аналитическим выражениям (15) и (23) с учётом распределения (24).

1.5. Магнитное поле соленоида и рабочая формула

Для того, чтобы воспользоваться формулой (4) для расчёта удельного заряда электрона, необходимо определить значение 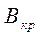в конкретном опыте. Это можно сделать с помощью косвенных измерений силы тока в конечном соленоиде, в который, вблизи его середины, соосно помещён ламповый диод.

Значение модуля вектора магнитной индукции в середине конечного соленоида можно оценить по формуле для бесконечного соленоида:

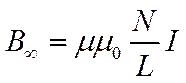, (25)

где 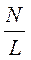- число витков на единицу длины, 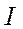– значение тока в соленоиде.

С учётом конструктивных особенностей лампового диода и катушки соленоида (экранирование поля цилиндрическим анодом, конечная длина катушки) фактическое значение магнитной индукции вблизи середины анода диода примерно вдвое меньше. Таким образом, если измерить критическое значение силы тока в конечном соленоиде, то, с учётом сделанного замечания, критическое значение магнитной индукции в диоде можно рассчитать по формуле:

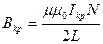(26)

Таким образом, если в формуле (17) учесть тот факт, что внешний радиус катода много меньше внутреннего радиуса анода, то мы получим окончательную рабочую формулу для нахождения удельного заряда электрона в виде:

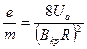(27)

Для расчёта по формулам (26), (27) принять следующие значения параметров:

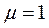- магнитная проницаемость,

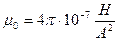- магнитная постоянная,

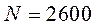- число витков в катушке соленоида,

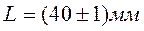- высота (длина) катушки соленоида,

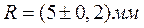- радиус цилиндрического анода лампового диода.