Решение. Изображенная на рисунке схема имеет два узла в точках А и С, а также три не разветвляющихся участка АВС

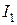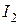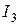Изображенная на рисунке схема имеет два узла в точках А и С, а также три не разветвляющихся участка АВС, АС и АDC. Это значит, что в цепи имеется три неизвестных силы тока , и . Для решения задачи воспользуемся правилами Кирхгофа. Произвольно выберем направления этих токов в каждом из соответствующих участков. Будем считать, что токи по участкам АВС, АС и АDC текут от узла А. Конечно, реально так быть не может: обязательно должен существовать хотя бы один ток, входящий в узел. Это следует из закона сохранения заряда. Однако, тем и удобны правила Кирхгофа, что их применение дает правильный результат даже при таком заведомо неправильном выборе направлений токов: те токи, направление которых случайно оказались выбранными правильно, получатся при решении положительными, а токи, направление которых противоположно предполагаемому, получатся отрицательными. Поскольку неизвестных токов три, то для их нахождения необходимо составить систему из трех независимых уравнений. Первое уравнение получим с помощью первого правила Кирхгофа, которое запишем для одного из двух узлов цепи, например, узла А.

.

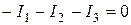При составлении уравнения все токи взяты со знаком минус, т. к. все они предполагаются выходящими из узла А.

Записывать теперь с помощью первого правила Кирхгофа следующее уравнение для узла С бессмысленно, так как получится линейно зависимое уравнение, отличающееся только тем, что все члены его умножены на минус единицу.

Два оставшихся уравнения можно составить с помощью второго правила Кирхгофа. Для этого мысленно выделяем в схеме замкнутые участки. Таких контуров в приведенной схеме три: ABCA, ACDA и ABCDA. Выберем, например, два первых и произвольно зададим направление обхода каждого из них. Будем обходить контуры ABCA и ACDA по направлению движения часовой стрелки. При составлении уравнений учтем, что отсутствие информации о величине внутреннего сопротивления источников тока в условии задачи позволяет предположить, что это сопротивление пренебрежимо мало. На схемах более длинным и тонким отрезком прямой обозначается положительный полюс источника тока, а коротким и толстым – отрицательный. Учитывая выбранные направления токов и направления обхода контуров, а также знаки полюсов источников тока, получим следующие два уравнения для контуров ABCA и ACDA соответственно:

,

.

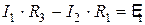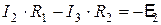Подставим в полученную систему трех уравнений численные значения сопротивлений и э.д.с., заданные в условии задачи.

.

,

.

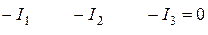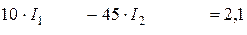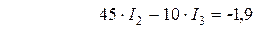Обратите внимание, что система уравнений записана таким образом, чтобы искомые токи с определенным значением индекса располагались друг под другом, образуя столбцы. В тех местах, где в столбце имеется пропуск, можно считать, что соответствующий ток умножен на нулевой коэффициент. Правая часть уравнений также образует свой столбец свободных членов. Сделано это для того, чтобы удобнее было использовать метод решения системы алгебраических уравнений с помощью определителей. Этот метод, предложенный швейцарским математиком Г. Крамером в 1750г., находит широкое применение для исследования и решения систем уравнений.

Составим определитель полученной системы:

.

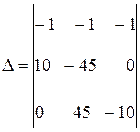Заменяя первый, затем второй и, наконец, третий столбец определителя системы столбцом свободных членов получаем еще три определителя

, , .

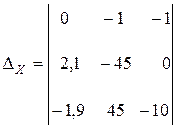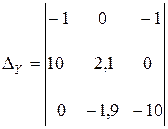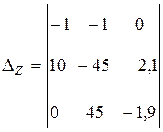Если в определителе системы 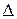нет ни одной пары строк с пропорциональными элементами и он не равен нулю, то решение системы единственно и определяется по формулам

, .

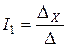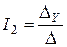
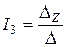Вычислить каждый определитель можно, пользуясь его свойствами по известному алгоритму: определитель равен сумме произведений элементов какой-либо строки (или какого–либо столбца) на их алгебраические дополнения. Алгебраическим дополнением элемента определителя называется его минор, взятый со своим или с противоположным знаком. Знак алгебраического дополнения определяется по следующему правилу: если сумма номеров столбца и строки, на пересечении которых стоит элемент, есть число четное, то минор берется со своим знаком, если нечетное, - то с противоположным. Вычисляя определитель удобно его раскладывать по строке (или по столбцу), содержащей нули.

Вычислим вначале определитель системы

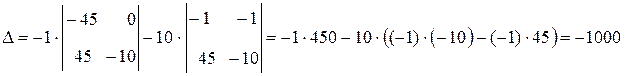Теперь вычислим определител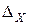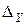и , и .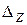

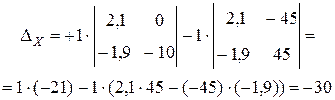
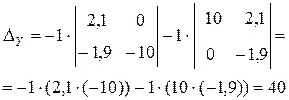
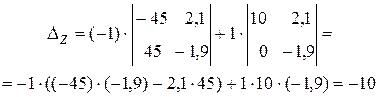
Вычислив определители по приведенным выше формулам, получим ответ: 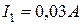, , 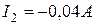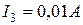. Отрицательный знак тока 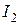говорит, что этот ток течет на самом деле от точки С к А. Направление же остальных токов было выбрано верно.