Решение. Поскольку шары расположены далеко друг от друга, то их можно считать уединенными
Поскольку шары расположены далеко друг от друга, то их можно считать уединенными. В этом случае их энергию можно определить по формулам (48):
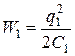 ,
,
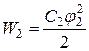 .
.
Емкость шара в вакууме определяется формулой
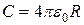 .
.
Следовательно, энергии шаров до их соединения равны
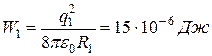 ,
,
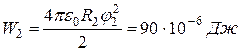 .
.
При соединении шаров проволокой они становятся единым проводником, потенциал которого, после установления равновесного распределения зарядов, во всех точках системы одинаков. При этом общий заряд сохраняется. Будем обозначать величины в конечном состоянии звездочкой. Тогда система уравнений для определения конечного потенциала и далее конечной энергии системы будет иметь вид:
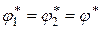
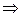
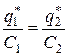 ,
,
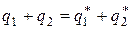 ,
,
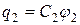 ,
,
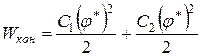 .
.
Решая систему, получим 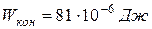 .
.
Энергия, которая выделится к моменту установления равновесного состояния, равна разности начальной и конечной электрической энергии системы:
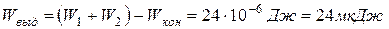 .
.
Тема 3. ЗАКОНЫ ПОСТОЯННОГО ТОКА
Основные понятия и соотношения
Электрический ток представляет собой направленное движение электрических зарядов. Носителями заряда в металлах являются валентные электроны, потерявшие связь со своими атомами в процессе образования кристаллической решетки. Принято считать, что направление тока определяется по направлению движения положительных носителей. Поэтому направление тока противоположно направлению движения электронов.
Понятие силы тока вводится для характеристики направленного движения зарядов в тонком проводнике. В общем случае в электрической схеме можно выделить точки, в которых сходятся не менее трех проводников. Такие точки называют узлами. Введем произвольно положительное направление на участке одного из проводов, соединяющего два соседних узла. Построим теперь функцию 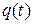 по следующему правилу: значение
по следующему правилу: значение 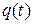 равно разности величины зарядов, прошедших через поперечное сечение проводника в положительном и отрицательном направлениях за время
равно разности величины зарядов, прошедших через поперечное сечение проводника в положительном и отрицательном направлениях за время 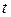 . Сила тока
. Сила тока 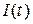 определяется как производная функции
определяется как производная функции 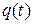 :
:
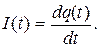
Если 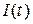 >0, то заряды движутся в положительном направлении, если
>0, то заряды движутся в положительном направлении, если 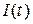 <0 - в отрицательном. Единица силы тока ампер: 1А = 1Кл/с.
<0 - в отрицательном. Единица силы тока ампер: 1А = 1Кл/с.
Если в проводнике имеется ток, то потенциал электрического поля в различных точках проводника не одинаков. Потенциал уменьшается в направлении движения положительных зарядов.
Для поддержания постоянного тока, т.е. движения электронов с постоянной средней скоростью, необходимо непрерывное действие на них силы. А это значит, что электроны в проводниках движутся с трением, или, иначе говоря, что проводники обладают электрическим сопротивлением.
Если состояние проводника остается неизменным (не меняется его температура и т.д.), то для каждого проводника или участка цепи, состоящего из нескольких проводников, существует однозначная зависимость между разностью потенциалов на концах участка и силой тока в нем. Она выражается законом Ома для участка цепи, не содержащего источников тока
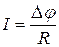 .
.
Коэффициент 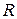 называется общим сопротивлением участка цепи и определяется по следующим формулам:
называется общим сопротивлением участка цепи и определяется по следующим формулам:
при последовательном соединении резисторов (участков цепи, обладающих заметным сопротивлением)
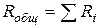 ,
,
при параллельном соединении резисторов
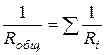 .
.
Сопротивление проводника зависит от его формы и вещества, из которого он изготовлен. Для проводника цилиндрической формы постоянного поперечного сечения
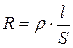 ,
,
где 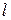 - длина проводника,
- длина проводника, 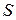 - площадь поперечного сечения проводника,
- площадь поперечного сечения проводника, 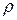 - удельное сопротивление вещества.
- удельное сопротивление вещества.
Чтобы поддерживать ток достаточно длительное время, нужно от конца проводника с меньшим потенциалом непрерывно отводить приносимые сюда током заряды (предполагается, что они положительные), а к концу с большим потенциалом их непрерывно подводить. Это означает, что в замкнутом контуре наряду с участками, на которых положительные носители тока движутся в сторону уменьшения потенциала, должны иметься участки, на которых перенос этих зарядов происходит в направлении возрастания потенциала, т.е. против сил электростатического поля. Перемещение носителей тока на этих участках возможно лишь с помощью сил неэлектростатического происхождения, называемых сторонними силами.
Сторонние силы можно охарактеризовать работой, которую они совершают при перемещении по цепи заряда. Величина, равная отношению работы 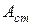 сторонних сил на некотором участке цепи 1-2, к тому заряду
сторонних сил на некотором участке цепи 1-2, к тому заряду 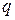 , над которым эта работа совершена, называется электродвижущей силой (э.д.с.)
, над которым эта работа совершена, называется электродвижущей силой (э.д.с.) 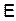 на данном участке:
на данном участке:
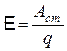 .
.
В общем случае, при перемещении заряда по участку цепи 1-2, над ним совершают работу как силы электростатической природы, так и сторонние. Величина 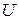 , равная отношению этой суммарной работы
, равная отношению этой суммарной работы 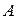 к заряду
к заряду 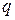 , над которым она совершена, называется падением напряжения или просто напряжением на данном участке цепи 1-2:
, над которым она совершена, называется падением напряжения или просто напряжением на данном участке цепи 1-2:
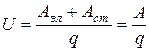 .
.
Используя связь разности потенциалов с работой электростатических сил и э.д.с. с работой сторонних сил, получаем формулу для напряжения в виде
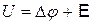 .
.
Для участка цепи 1-2, содержащего источник э.д.с., закон Ома имеет вид
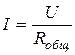 .
.
Если участок цепи замкнут, то точки 1 и 2 соединены, и, следовательно, имеют равные потенциалы. В этом случае закон Ома приобретает вид
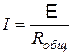 .
.
Если внешнее сопротивление замкнутой цепи равно нулю, то в ней протекает ток короткого замыкания:
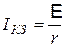 ,
,
где 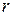 - внутреннее сопротивление источника тока.
- внутреннее сопротивление источника тока.
Расчет разветвленных цепей значительно упрощается, если пользоваться правилами, сформулированными Кирхгофом.
Первое правило относится к узлам электрической цепи. Алгебраическая сумма токов, сходящихся в узле, равна нулю:
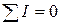 .
.
При этом ток, текущий к узлу, считается имеющим один знак (плюс или минус), а ток, текущий от узла - другой.
Второе правило относится к любому, мысленно выделенному в разветвленной цепи, замкнутому контуру.
При обходе контура алгебраическая сумма напряжений на каждом его неразветвленном участке равна алгебраической сумме э.д.с., действующих в контуре:
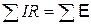 .
.
При составлении уравнений направление обхода контура выбирается произвольно. Произведение силы тока на сопротивление считается положительным, если направление тока, также предварительно выбранное произвольно, совпадает с направлением обхода контура, отрицательным, если не совпадает. Э.д.с. берут положительной, если она действует на положительные носители тока в направлении обхода, и берут отрицательной, если - наоборот.
Поскольку общая работа электростатических и сторонних сил на участке цепи 1-2 равна
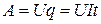 ,
,
то для мощности, развиваемой током на этом участке, получим
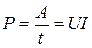 .
.
Эта мощность может расходоваться на совершение работы над внешними телами (при этом проводник должен перемещаться в пространстве), на протекание химических реакций и, наконец, на нагревание данного проводника.
В последнем случае, после установления теплового равновесия нагреваемого током проводника с окружающей средой, работа тока будет равна количеству выделяемого проводником тепла:
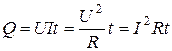 .
.
Соотношение называется законом Джоуля-Ленца.
Если сила тока изменяется со временем, то количество тепла определяется по формуле
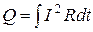 .
.
Из закона Ома для замкнутой цепи получаем
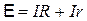 ,
,
где 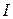 - сила тока,
- сила тока, 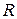 - внешнее сопротивление,
- внешнее сопротивление, 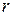 - внутреннее сопротивление источника тока. Умножив левую и правую части этого выражения на
- внутреннее сопротивление источника тока. Умножив левую и правую части этого выражения на 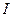 , получим
, получим
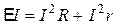 .
.
Здесь 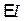 - полная мощность источника
- полная мощность источника 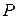 ;
; 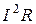 - полезная мощность
- полезная мощность 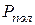 , которая выделяется (рассеивается) на внешнем сопротивлении;
, которая выделяется (рассеивается) на внешнем сопротивлении; 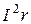 - мощность потерь
- мощность потерь 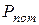 , которая выделяется на внутреннем сопротивлении источника.
, которая выделяется на внутреннем сопротивлении источника.
Выразив, с помощью закона Ома, полезную мощность через сопротивление
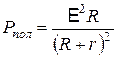 ,
,
и исследовав эту функцию на максимум, можно показать, что наибольшая полезная мощность выделяется при равенстве внешнего сопротивления внутреннему: 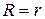 .
.
Отношение полезной мощности 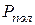 к полной мощности
к полной мощности 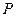 , развиваемой источником э.д.с., называется коэффициентом полезного действия (КПД)
, развиваемой источником э.д.с., называется коэффициентом полезного действия (КПД) 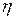 этого источника:
этого источника: 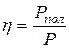 .
.
Дата добавления: 2015-02-16; просмотров: 709;
