Решение. Рассмотрим сначала первый случай, когда заряд на обкладках является постоянным

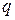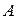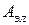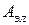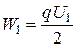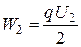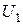Рассмотрим сначала первый случай, когда заряд на обкладках является постоянным. Работа внешних сил по удалению диэлектрика из конденсатора равна взятой с обратным знаком работе электрических сил . Согласно закону сохранения энергии работу электрических сил можно определить как разность между начальной энергией конденсатора и конечной , где и 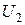- соответственно начальное (без диэлектрика) и конечное ( с диэлектриком) значения напряжения на конденсаторе. Следовательно,

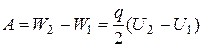. (53)

Чтобы найт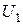и и 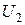, воспользуемся известными выражениями для напряженности электрического поля 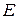между обкладками плоского конденсатора:

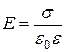в диэлектрике,

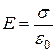вне диэлектрика, (54)

где 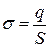- поверхностная плотность заряда. Подставляя данные выражения в формулу для 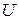получим

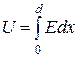, (55)

где направление оси 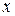выбирается ортогональным плоскости обкладок, получим

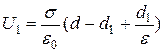, (56)

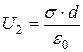, (57)

и как следствие

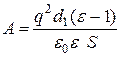. (58)

Рассмотрим теперь второй случай, когда напряжение на обкладках 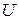поддерживается постоянным (например, за счет подключенного к конденсатору внешнего источника питания). Как и в предыдущем случае, работа 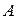по удалению диэлектрика из конденсатора будет равна взятой с обратным знаком работе электрических сил 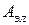.Однако последняя в данном случае будет определяться иначе:

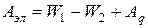, (59)

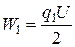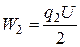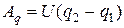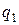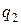где - начальная энергия конденсатора, - конечная, - работа по переносу заряда от источника питания, а и - соответственно начальный и конечный заряд на конденсаторе.

Следовательно,

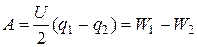. (60)

Определяя заряды 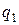и 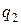из выражения для 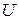, которые по аналогии с предыдущим случаем можно записать в виде

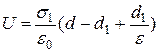, (61)

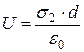, (62)

где 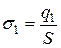и 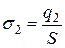, получим

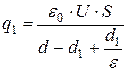; (63)

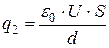, (64)

и как следствие

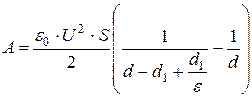. (65)