Решение. Физическая система состоит из бесконечного линейно распределенного заряда и созданного им поля

Физическая система состоит из бесконечного линейно распределенного заряда и созданного им поля. Решим задачу двумя методами. Применим сначала теорему Гаусса. В силу симметрии вектор напряженности в любой точке нормален цилиндрической поверхности, проходящей через эту точку и имеющей ось симметрии, совпадающую с нитью. Поэтому в качестве замкнутой поверхности возьмем цилиндр длиной 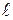с осью симметрии, совпадающей с нитью, боковая поверхность которого проходит через точку А (рис.7). Поток вектора 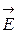через торцы цилиндра равен нулю, через боковую поверхность 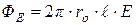. Полный заряд, расположенный внутри цилиндра, 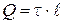. С учетом этого по теореме Гаусса будем иметь

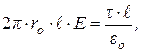
откуда 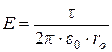(27)

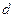
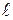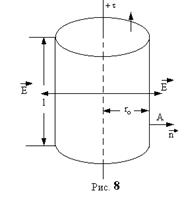
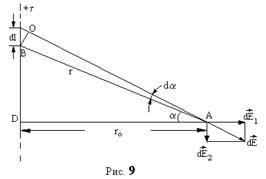
Теперь применим принцип суперпозиции. Разделим нить на столь малые элементы , чтобы заряд 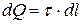, находящийся на каждом таком элементе, можно было считать точечным. Выберем один из элементов (рис.8). В точке А он создает напряженность:

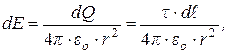(28)

где r - расстояние от выбранного элемента до точки А.

Разложим вектор 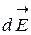на нормальную 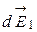и тангенциальную 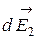составляющие. Из рис.8 видно, что

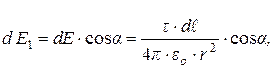(29)

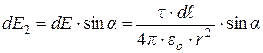. (30)

Поскольку положение выбранного точечного заряда на нити определяется углом 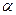, возьмем угол в качестве переменной интегрирования. В связи с этим выразим входящие в (29) и (30) величины 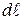и r через r_o и .

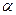Из треугольника АDВ находим 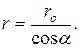Из треугольника ВСО следует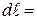 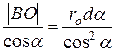, так как .

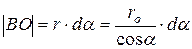Подставив найденные значения в уравнения (29) и (30), получим

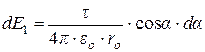(31)

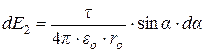(32)

Интегрируя (31) и (32) в пределах от - 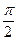до + 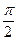будем иметь

.

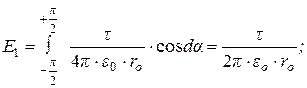
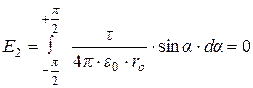Таким образом, окончательно 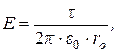что совпадает с выражением, полученным с помощью теоремы Гаусса.

Нетрудно видеть, что в данном случае вычисления по принципу суперпозиции оказались более трудоемкими, чем при использовании теоремы Гаусса. Однако существуют задачи, в которых все наоборот.